高校数学の「座標と直線」に関する問題を解いてみる。(Yahoo!知恵袋より)

(1) \(a\)の値のとりうる範囲を求めよ。
(2) 直線\( \ \mathrm{AB} \ \)と\( \ x\)軸との交点の座標を求めよ。
(3) 原点\(\mathrm{O}\)と\( \ \mathrm{A}, \ \mathrm{B} \ \)を頂点とする三角形の面積が\( \ 1 \ \)であるとき、\(a\)の値を求めよ。
定数 a は0以外の実数

Lukia
ある程度は数字と同じように扱ってもいいのですが、少し注意しておかねばならないこともあります。
定数\( \ a \ \)は「実数」と定められている場合、符号に関していうと、「\(+\)(プラス)」でも、「\(-\)(マイナス)」でもいいのです。
またどちらの符号もつかない\(0\)だってありえますね。

Lukia
定数\(a\)を正の数だと勝手に判断してしまう人がいます。
「だって~、マイナスついてないし~」と思うかもしれませんが、
\(a \gt 0\) という条件がついていない以上、
\(a \lt 0\)の場合も考えるべきであり、さまざまなケースを想定できる人かどうかが問われているといえます。

Lukia
それは\( \ 0 \ \)です。
2点\( \ \mathrm{A}, \ \mathrm{B} \ \)は\(x\)軸をはさんで反対側にある。ということですから、
$$\begin{align}2点 \ &\mathrm{A}, \ \mathrm{B}が互いに \ x軸の反対側にあるためには, \\ a \neq 0 \ &かつ \ -2a-1 \neq 0 \\ すなわち&a \neq 0 \ かつ \ a \neq -\frac{1}{2} \ である必要がある. \end{align}$$
Ⅰ
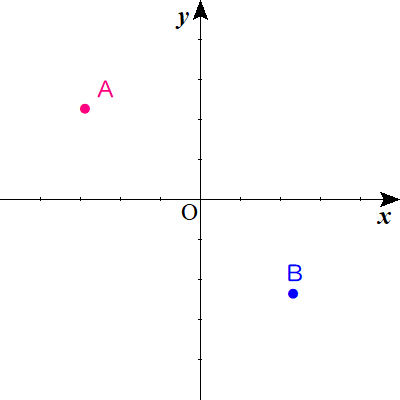
$$\begin{align}a \gt &0 \ のとき\quad \quad \cdots \ ⅰ \\ 点\mathrm{B} \ は&明らかに第2象限にある.\\ 点\mathrm{B}のx座標&より,\quad -2a-1 \lt 0\\ すなわち& \ -\frac{1}{2} \lt a\quad \quad \cdotsⅱ\\ また点\mathrm{A}は,&-a+1 \gt 0\\ すなわち& \ 0 \lt a \lt 1\quad のとき \ 第1象限にあり\quad \quad \cdots ⅲ\\ &1 \lt a \ のとき, \ 第4象限にある\quad \quad \cdots ⅳ \\ ⅰからⅳより,&\quad 0 \lt a \lt 1, \ または \ 1 \lt a \end{align}$$
Ⅱ
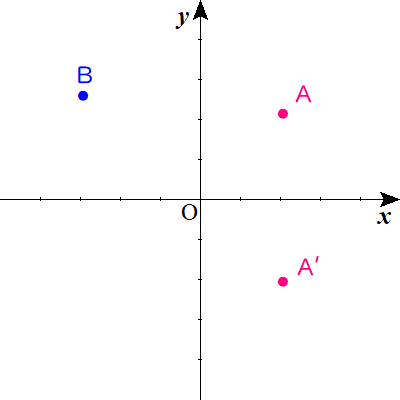
$$\begin{align}a \lt 0&\quad かつ \ a \neq -\frac{1}{2}\quad のとき\quad \quad \cdots ⅰ \\ 点\mathrm{A}は,&明らかに第2象限に存在する. \\ ゆえに& \ 点\mathrm{B} \ は第4象限に存在する. \\ 点\mathrm{A}のy座標より,&\quad -a+1 \gt 0\\ すなわち&\quad 1 \gt a\quad \quad \cdots ⅱ\\ 点\mathrm{B}のx座標より,&\quad -2a-1 \gt 0\\ すなわち&\quad -\frac{1}{2} \gt a\quad \quad \cdots ⅲ\\ ⅰからⅲより,&\quad a \lt -\frac{1}{2}\end{align}$$
$$\begin{align}Ⅰ,Ⅱ \ より,&\quad 求める \ a \ の値の範囲は \\ a \lt -\frac{1}{2}&\quad または \ 0 \lt a \lt 1\quad または \ 1 \lt a \end{align}$$
(2)
$$\begin{align}直線 \ \mathrm{AB} \ は \ &y=\frac{-3a+1}{3a+1}\left( x-a\right)-a+1\quad と表せる. \\ 直線 \ \mathrm{AB} \ &が \ x軸と交わるのは, \ y=0 \ のとき.\\ \frac{-3a+1}{3a+1}\left( x-a\right)-a+1=&0\\ \frac{-3a+1}{3a+1}\left( x-a\right)=&a-1 \\ ここで,&3a+1 \neq 0\quad かつ\quad -3a+1 \neq 0 \\ すなわち,&a \neq -\frac{1}{3}\quad かつ\quad a \neq \frac{1}{3} \ とする.\\ 両辺を \ &\frac{3a+1}{-3a+1} \ 倍する.\\ x-a=&\left( a-1\right)\cdot \frac{3a+1}{-3a+1}\\ x=&\frac{\left( a-1\right)\left( 3a+1\right)+a\left( -3a+1\right)}{-3a+1} \\ x=&\frac{a+1}{3a-1}\\ 求める座標は, \ &\left( \frac{a+1}{3a-1} \ , \ 0\right) \end{align}$$
(3)
$$\begin{align}\triangle \mathrm{OAB}の面積 \ \mathrm{S} \ は,&線分\mathrm{AB}を底辺とし, \\ \ &直線\mathrm{AB}と原点\mathrm{O}との距離を高さhとして求められる。\\ \mathrm{S}=&\frac{1}{2}\vert \mathrm{AB} \vert h=1 \\ \vert \mathrm{AB} \vert h=&2\quad \quad \cdots \ ★\end{align}$$
$$\begin{align}\vert \mathrm{AB} \vert=&\sqrt{\left( a+2a+1\right)^2+\left( -a+1-2a\right)^2} \\ =&\sqrt{18a^2+2} \end{align}$$
$$\begin{align}また \ 直線 \ \mathrm{AB} \ は, \ &a \neq -\frac{1}{3} \ のとき, \\ &\left( -3a+1\right)x-\left( 3a+1\right)y+a+1=0\quad と表せる. \\ h=&\frac{\vert a+1 \vert}{\sqrt{\left( -3a+1\right)^2+\left( 3a+1\right)^2}}=\frac{\vert a+1 \vert}{\sqrt{18a^2+2}} \end{align}$$
★に代入する.
$$\begin{align}\vert \mathrm{AB} \vert h=&2 \\ \sqrt{18a^2+2}\cdot \frac{\vert a+1 \vert}{\sqrt{18a^2+2}}=&2 \\ \vert a+1 \vert=&2 \end{align}$$
$$\begin{align}-1 \lt &a\quad のとき,\quad a+1=2\quad すなわち \ a=1 \\ a \leq &-1\quad のとき,\quad -a-1=2\quad すなわち \ a=-3\\ \\ ここで,&(1)で求めた \ a \ の値の範囲と \ a \neq -\frac{1}{3} \ と合わせて考える.\\ (1)より,&a \neq 1 \ であるので,\\ &a=1 \ は不適.\\ ゆえに&求める定数 \ a \ の値は \ a=-3\end{align}$$










ディスカッション
コメント一覧
まだ、コメントがありません