高校数学の「2つの放物線に囲まれた区間の面積」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年2月8日2020年9月10日微分と積分Yahoo!知恵袋,数学,数学検定,数検2級

読了時間: 約2分39秒

KEYWORDS高校数学 , 積分 , 数学検定2級

Contents

1. 問題
2. こたえ

問題

2つの曲線$ \ y=x^2-4\quad \left( -1 \leq x \leq 3\right) \ $,$ \ y=-x^2+2x\quad \left( -1 \leq x \leq 3\right) \ $と直線$ \ x=3 \ $で囲まれた2つの部分の面積の和$ \ \mathrm{S} \ $を求めよ.

$$\begin{align}f\left( x\right)=&\color{#0004fc}{x^2-4}-\left( \color{#f700ca}{-x^2+2x}\right)=2x^2-2x-4\quad とする. \ f\left( x\right)=&0\quad となるのは, \ x=&-1\quad ,\quad x=2 \end{align}$$
ゆえにグラフは以下の通り.

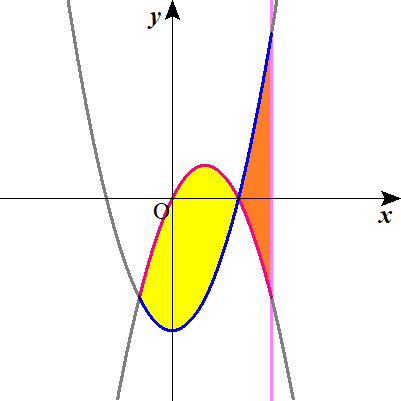
$$\begin{align}ここで,\quad \quad &-1 \leq x \leq 2\quad の区間の面積を \ \mathrm{S}_1\quad とし, \ &2 \leq x \leq 3\quad の区間の面積を \ \mathrm{S}_2\quad とする.\end{align}$$

Lukia

黄色で塗りつぶされた部分が$ \ \mathrm{S}_1 \ $,
オレンジ色で塗りつぶされた部分が$ \ \mathrm{S}_2 \ $です。

$$\begin{align}\int_{\beta}^{\alpha} f\left( x\right) dx=&\mathrm{F}\left( \alpha\right)-\mathrm{F}\left( \beta\right) \quad であり,\ \mathrm{F}\left( x\right)=&\frac{1}{3}\left( 2x^3-3x^2-12x\right)+\mathrm{C}\quad \left( \mathrm{C}\quad は積分定数\right) \quad である.\end{align}$$

Lukia

$ \ \begin{align}\mathrm{S}=&\mathrm{S}_1+\mathrm{S}_2 \\\\ =&\int_{-1}^{2} -f\left( x\right) dx+\int_{2}^{3} f\left( x\right) dx \\\\ =&\color{#0004fc}{-}\int_{-1}^{2} f\left( x\right) dx+\int_{2}^{3} f\left( x\right) dx\\\\ =&\color{#0004fc}{-}\lbrace \mathrm{F}\left( 2\right)-\mathrm{F}\left( -1\right)\rbrace + \mathrm{F}\left( 3\right)-\mathrm{F}\left( 2\right)\\\\ =&-2\mathrm{F}\left( 2\right)+\mathrm{F}\left( -1\right) +\mathrm{F}\left( 3\right)=\frac{38}{3} \end{align} \ $

Lukia

ちょっと手間なようですが、前もって$ \ f\left( x\right) \ $とその原関数（$ \ f\left( x\right) \ $を積分した関数）を求めておくと、煩雑な計算が少しだけ楽になります。

Lukia

また、本来ならば、$ \ -1 \leq x \leq 2\ $の区間については、
$ \ \frac{1}{6} \ $公式が使えますね。
今回は、$ \ \mathrm{S}_1 \ $と$ \ \mathrm{S}_2 \ $を別々に求めたほうが楽かもしれません。
二つの求積法をやってみて、自分の計算のスピードや確実さなどから、どっちがよいか試してみてください。