3つの集合問題はカルノー図で簡単解決!(準備編)【ビジネス数学検定2級 合格への道】

第75回 ビジネス数学検定受検まで あと56日
受検勉強を再開した2022年4月18日より16日経過しています。 
ビジネス数学検定2級の公式問題集の中で、ここは数学の知識があるほうが解きやすいなという問題について、
いくつか紹介してみたいと思います。
|
|
3つの集合問題はカルノー図で簡単解決!(準備編)
3つの集合問題、得意ですか?
私は、かなり苦手でした。
重なっているところを「かつ(\( \ \cap \ \))」や「または(\( \ \cup \ \))」、さらに「〜ではない(\( \ \overline{A} \ \))」などの記号を用いて表すうち、だんだんこんがらがってくるからです。
集合2つでも結構めんどくさいのに、3つになったら、混乱しないわけがありません。(笑)
そんな困っていた私ですが、ある日「カルノー図」を知ったことで、らくらく解決できるようになりました。
今回は、ベン図とカルノー図を対応させ、数式にあらわしてみたいと思います。

Lukia
ベン図をカルノー図に対応させる
3つの集合を、それぞれ\( \ \mathrm{X} \ \)、\( \ \mathrm{Y} \ \)、\( \ \mathrm{Z} \ \)とし、全体集合を\( \ \mathrm{U} \ \)とします。
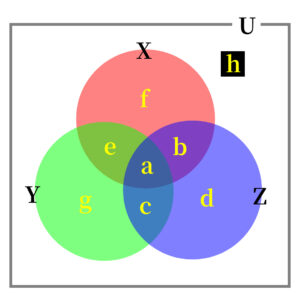 これをカルノー図(図というよりかは表ですね)にあらわしていきます。
これをカルノー図(図というよりかは表ですね)にあらわしていきます。
まず、\( \ \mathrm{X} \ \)、\( \ \mathrm{Y} \ \)の組み合わせを4通り作り、これに\( \ \mathrm{Z} \ \)の組み合わせをかけて、8通りの組み合わせで表します。
条件\( \ \mathrm{X} \ \)には、「集合\( \ \mathrm{X} \ \)に含まれる」、「集合\( \ \mathrm{X} \ \)に含まれない」の2通りが考えられます。
これは条件\( \ \mathrm{Y} \ \)や条件\( \ \mathrm{Z} \ \)にも同様に2通りずつありますので、
すべての組み合わせは、\( \ 2^3=8 \ \)通りあることになります。
横に5マス、縦に3マスの表を作ります。
上段に、「集合\( \ \mathrm{X} \ \)に含まれ、集合\( \ \mathrm{Y} \ \)にも含まれる」すなわち\( \ \mathrm{XY} \ \)
「集合\( \ \mathrm{X} \ \)に含まれるが、集合\( \ \mathrm{Y} \ \)には含まれない」すなわち\( \ \mathrm{X\overline{Y}} \ \)
「集合\( \ \mathrm{X} \ \)に含まれないが、集合\( \ \mathrm{Y} \ \)には含まれる」すなわち\( \ \mathrm{\overline{X}Y} \ \)
「集合\( \ \mathrm{X} \ \)に含まれず、集合\( \ \mathrm{Y} \ \)にも含まれない」すなわち\( \ \mathrm{\overline{X}\overline{Y}} \ \)
の項目を書き込みます。
2段めと3段目の一番左のマスに、「集合\( \ \mathrm{Z} \ \)に含まれる」すなわち\( \ \mathrm{Z} \ \)、
「集合\( \ \mathrm{Z} \ \)に含まれない」すなわち\( \ \mathrm{\overline{Z}} \ \)をそれぞれ書き込みます。
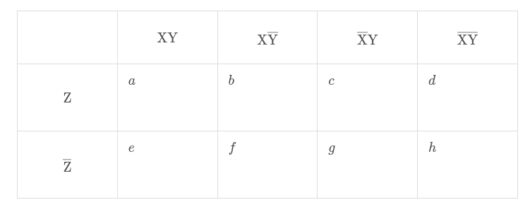
これでカルノー図の完成です。
8つの組み合わせに\( \ a \ \)~\( \ h \ \)までの文字を充てておきます。
数式にあらわしてみる
ベン図とカルノー図の\( \ a \ \)~\( \ h \ \)はそれぞれ対応させています。(じっくり見てくださいね)

 ベン図を見ると、集合\( \ \mathrm{X} \ \)、集合\( \ \mathrm{Y} \ \)、集合\( \ \mathrm{Z} \ \)は、それぞれ
ベン図を見ると、集合\( \ \mathrm{X} \ \)、集合\( \ \mathrm{Y} \ \)、集合\( \ \mathrm{Z} \ \)は、それぞれ
\( \ \mathrm{X}=a+b+e+f \ \)
\( \ \mathrm{Y}=a+c+e+g \ \)
\( \ \mathrm{Z}=a+b+c+d \ \)
と表せることがわかります。
集合\( \ \mathrm{Z} \ \)に関しては、カルノー図の\( \ \mathrm{Z} \ \)の列とぴったり符合していますね。
$$\begin{align}\mathrm{X}+\mathrm{Y}+\mathrm{Z}=&\left( a+b+e+f\right)+\left( a+c+e+g\right)+\left( a+b+c+d\right) \\\\ =&3a+2\left( b+c+e\right)+\left( d+f+g\right) \end{align}$$
また、\( \ \mathrm{X}\cup\mathrm{Y}\cup\mathrm{Z} \ \)(\( \ \mathrm{X} \ \)または\( \ \mathrm{Y} \ \)または\( \ \mathrm{Z} \ \))は、 $$\begin{align}\mathrm{X}\cup\mathrm{Y}\cup\mathrm{Z}=&a+b+c+d+e+f+g\\\\ =&a+\left( b+c+e\right)+\left( d+f+g\right) \\\\ =&\mathrm{U}-h\end{align}$$ であることがいえます。 この2つの式はすごく便利なので覚えておきましょう。

Lukia
私は、以下の図のようにして覚えています。
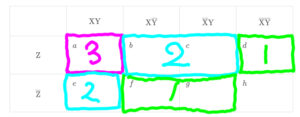
乱暴な話ですが、
なんならこのカルノー図と倍数の配置を覚えておけば、
上記の式を覚えられなくてもなんとかなります。(笑)
カルノー図に慣れたら、ベン図を描く必要はなくなりますので、
かなり素早く、クリアーに問題が解けるようになりますよ。
ビジネス数学検定2級 合格への道の記事一覧

[subscribe2]
よろしければ,アンケートに御協力ください。
アンケートでは、お読みになったタイトルをうかがいますので、御確認ください。
この記事のタイトルは『 3つの集合問題はカルノー図で簡単解決!(準備編)』です。

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/01eafba5.e8fec6de.03acf48d.1cc4eb39/?me_id=1213310&item_id=18590681&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F7431%2F9784822237431.jpg%3F_ex%3D240x240&s=240x240&t=picttext)










ディスカッション
コメント一覧
まだ、コメントがありません