高校数学の「二次関数の最大値・最小値」に関する問題を解いてみる。(Yahoo!知恵袋より)

読了時間: 約2分17秒
[mathjax]
問題
\(a\)を定数とする。
関数\(y=3x^2-6ax+2\)
\(\left( 0 \leq x \leq 2\right)\)について最小値を求めよ。
関数\(y=3x^2-6ax+2\)
\(\left( 0 \leq x \leq 2\right)\)について最小値を求めよ。
二次関数を見たら、まずは「平方完成」して軸と頂点を求める。

Lukia
二次関数は、とにかく軸と頂点の意識が何より大切です。
ですから、まずは平方完成してみましょう。
ですから、まずは平方完成してみましょう。
$$\begin{align}y=&f\left( x\right) とする。 \\\\ f\left( x\right)=&3\left( x^2-2ax\right)+2 \\\\ =&3\left( x-a\right)^2-3a^2+2 \end{align}$$

れもん
軸は、\(x=a\)で、
頂点は、\(\left( a , -3a^2+2\right)\)とわかりますね。
頂点は、\(\left( a , -3a^2+2\right)\)とわかりますね。

れもん
でも、\(a\)っていくつだかわからないですよね。

Lukia
\(a\)がはっきりと定まっていないわけですから、
定義域と、軸との位置関係を見ていく必要があるということです。
定義域と、軸との位置関係を見ていく必要があるということです。

Lukia
定義域と軸の関係を表すと以下の図のような5通りが考えられます。
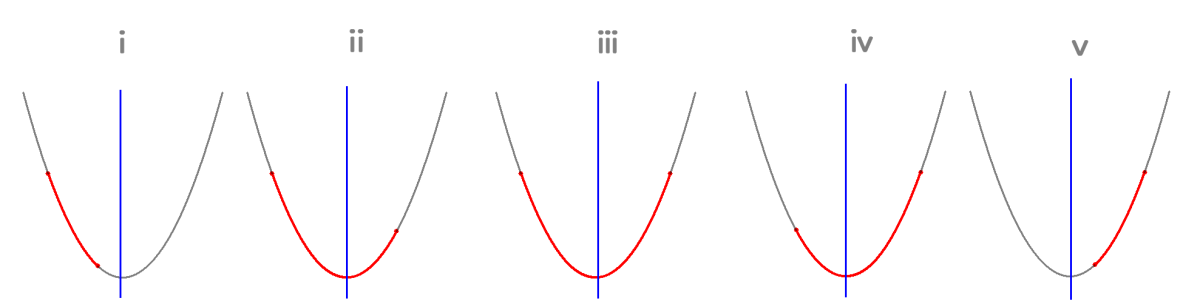
| ⅰ | ⅱ | ⅲ | ⅳ | ⅴ | |
| 軸の位置 | $$2 \lt a$$ | $$1 \leq a \leq 2$$ | $$a=1$$ | $$0 \leq a \leq 1$$ | $$a \lt 0$$ |
| 最大値 | $$f\left( 0\right)$$ | $$f\left( 0\right)$$ | $$f\left( 0\right)$$ または $$f\left( 2\right)$$ |
$$f\left( 2\right)$$ | $$f\left( 2\right)$$ |
| 最小値 | $$f\left( 2\right)$$ | $$f\left( a\right)$$ | $$f\left( a\right)$$ | $$f\left( a\right)$$ | $$f\left( 0\right)$$ |

れもん
今回の問題は、最小値を求めるのですから、場合分け自体は5通りあるけれど、
答えの場合分けは3通りになるんですね。
答えの場合分けは3通りになるんですね。

Lukia
そうですね。
今回は、下に凸の関数なので、軸に近い端点か、頂点そのものが最小値を取ります。
また、今回は関係ないけれど、軸よりも離れている端点が最大値を取ります。
今回は、下に凸の関数なので、軸に近い端点か、頂点そのものが最小値を取ります。
また、今回は関係ないけれど、軸よりも離れている端点が最大値を取ります。
$$\begin{align}ⅰ) &2 \lt a のとき \\\\ f\left( 2\right)=&3\left( 2-a\right)^2-3a^2+2 \\\\ =&14-12a \end{align}$$
$$\begin{align}ⅱ) &0 \leq a \leq 2 のとき \\\\ f\left( a\right)=&-3a^2+2 \end{align}$$
$$\begin{align}ⅲ) &a \geq 0 のとき \\\\ f\left( 0\right)=&2 \end{align}$$
こたえ
| ⅰ) | $$2 \lt a のとき$$ | $$14-12a$$ |
| ⅱ) | $$0 \leq a \leq 2 のとき$$ | $$-3a^2+2$$ |
| ⅲ) | $$a \geq 0 のとき$$ | $$2$$ |
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません