高校数学の「等差×等比数列の和」に関する問題を解いてみる。（Yahoo!知恵袋より）
[mathjax]
等差数列\(\lbrace a_n\rbrace\) が \(a_{n}=2n+1\) であり、
等比数列\(\lbrace {b}_{n}\rbrace\) が \({b}_{n}=2^n\) であるとき、$$S_{n}=\sum_{k=1}^{n}{a_k\cdot b_k}\quad を求めよ。$$
「公式」を頭にたたきこめ！
Lukia
大まじめに計算すると、おそろしく時間がかかるので、できるだけ公式っぽくして覚えてしまいましょう。
$$\begin{align}公差がdの等差数列 \ \lbrace a_n\rbrace \ と,\\\\ 初項が{b}_1 \ \left( ただし \ {b}_1 \neq 0\right)公比がr \ \left( ただしr \neq 0 \ , \ r \neq 1\right) \ の等比数列 \ \lbrace {b}_n\rbraceを考える.\end{align}$$
$$ S_n=\sum_{k=1}^{n}{a_k\cdot b_k}\quad とする.$$
$$S_n=a_1b_1+a_2b_2+a_3b_3+\cdots+a_{n-1}b_{n-1}+a_nb_n\quad とおける.$$
$$両辺に \ r \ をかけて、辺々引く.$$
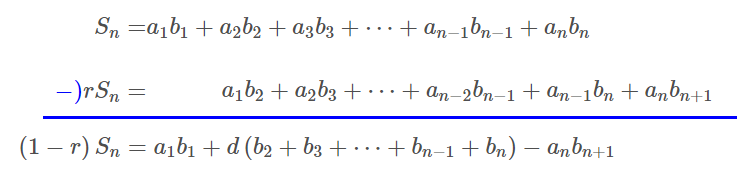
$$\begin{align}\left( 1-r\right)S_n=&a_1b_1+d\left( b_{\color{red}{2}}+b_3+\cdots+b_{n-1}+b_n\right)-a_nb_{n+1} \\\\ =&a_1b_1+d\sum_{k={\color{red}{2}}}^{n}{b_k}-a_nb_{n+1} \\\\ =&a_1b_1+d\cdot \left( \frac{b_{\color{red}{2}}-b_n\cdot r}{1-r}\right)-a_nb_{n+1} \end{align}$$
Lukia
何も手につかないとか、式の操作の理解ができないとか、人によっていろんな事情があると思います。
でも、そんな時こそ、まずは公式を覚えてしまって、手持ちの問題集で数値を変えて、ガシガシ練習するのです。
何度かくりかえすと、ふっと理解できることがあります。（まぁ、数時間、数日単位ではないですけどね。）
いざ、問題にあてはめてみよう。
$$\begin{align}等差数列&\lbrace a_n\rbrace \ の公差は \ {\color{red}{2}},\quad \\\\等比数列& \lbrace b_n\rbrace \ の公比は \ {\color{#0004fc}{2}} \ であるから \\\\ \left(1-\color{#0004fc}{2}\right)S_n=&3\cdot 2+{\color{red}{2}}\cdot \left( \frac{b_{\color{#ff00ff}{2}}-b_n\cdot {\color{#0004fc}{2}}}{1-{\color{#0004fc}{2}}}\right)-\left( 2n+1\right)2^{n+1} \\\\ -S_n=&6+\left( \frac{8-2\cdot 2^{n+1}}{-1}\right)-\left( 2n+1\right)2^{n+1}\\\\ =&-2-\left( 2n-1\right)2^{n+1}\\\\ \\\\ S_n=&2+\left( 2n-1\right)2^{n+1}\end{align}$$
こたえ
$$S_n=2+\left( 2n-1\right)2^{n+1}$$
共有:
プロフィール
