2019年大学入試センター試験 数学2B「第1問 指数・対数」を解いてみる。
[mathjax]
\( \ \log_{2}\left( x+2\right)-2\log_{4}\left( y+3\right)=-1 \quad \cdots\cdots \ ② \ \)
\( \ \left( \frac{1}{3}\right)^y-11\left( \frac{1}{3}\right)^{x+1}+6=0\quad \cdots\cdots \ ③ \ \)
を満たす実数\( \ x \ , \ y \ \)を求めよう。
真数の条件により,\( \ x \ , \ y \ \)のとり得る値の範囲は\( \ \color{#0004fc}{タ} \ \)である。（中略）
ただし,対数\( \ \log_{a}b \ \)に対し,\( \ a \ \)を底といい,\( \ b \ \)を真数という。
真数は常に正であるので,
$$\begin{align}x+2 \gt 0& \ \ かつ \ \ y+3 \gt 0 \\\ \color{#0004fc}{x \gt -2}& \ \ かつ \ \ \color{#0004fc}{y \gt -3}\end{align}$$\
\( \ \log_{4}\left( y+3\right)=\frac{\log_{2}\left( y+3\right)}{\color{#0004fc}{チ}} \ \) である。
よって, ②から
\( \ y=\color{#0004fc}{ツ}x+\color{#0004fc}{テ}\quad \cdots\cdots \ ④ \ \) が得られる。
$$\begin{align}\log_{4}\left( y+3\right)=&\frac{\log_{2}\left( y+3\right)}{\log_{2}2^2}=\frac{\log_{2}\left( y+3\right)}{\color{#0004fc}{2}}\end{align}$$
これを②に代入する。
$$\begin{align}\log_{2}\left( x+2\right)-2\log_{4}\left( y+3\right)=&-1 \\\\ \log_{2}\left( x+2\right)-2\cdot \frac{\log_{2}\left( y+3\right)}{2}=&-\log_{2}2 \\\\ \log_{2}\left( y+3\right)=&\log_{2}\left( x+2\right)+\log_{2}2=\log_{2}2\left( x+2\right)\\\\ \ y+3=&2\left( x+2\right)\\\\ y=&\color{#0004fc}{2}x+\color{#0004fc}{1}\quad \cdots\cdots \ ④ \end{align}$$
\( \ t^2-\color{#0004fc}{トナ}t+\color{#0004fc}{ニヌ}=0\quad \cdots\cdots \ ⑤ \ \) が得られる。
また,\( \ x \ \)が\( \ x \gt -2 \ , \ y \gt -3 \ \)における\( \ x \ \)の範囲を動くとき,\( \ t \ \)のとり得る値の範囲は
\( \ \color{#0004fc}{ネ} \lt t \lt \color{#0004fc}{ノ}\quad \cdots\cdots \ ⑥ \ \) である。
$$\begin{align}\left( \frac{1}{3}\right)^y-11\left( \frac{1}{3}\right)^{x+1}+6=&0\quad \cdots\cdots \ ③ \\\\ \left( \frac{1}{3}\right)^{2x+1}-\frac{11}{3}\left( \frac{1}{3}\right)^x+6=&0 \\\\ \frac{1}{3}\left( \frac{1}{3}\right)^{2x}-\frac{11}{3}\left( \frac{1}{3}\right)^x+6=&0\\\\ \left( \frac{1}{3}\right)^{2x}-11\left( \frac{1}{3}\right)^x+18=&0\\\\ \ t^2-\color{#0004fc}{11}t+\color{#0004fc}{18}=&0\quad \cdots\cdots \ ⑤ \end{align}$$
$$t=\left( \frac{1}{3}\right)^x\quad \left( -2 \lt x\right)\quad のグラフは以下の通り。$$
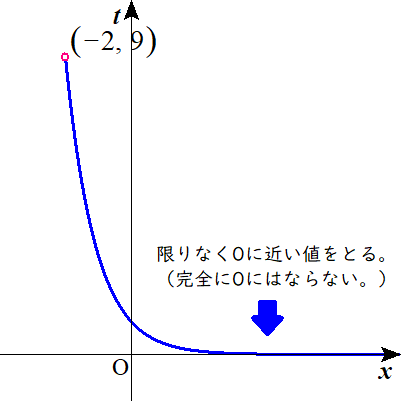
$$ゆえに\quad \color{#0004fc}{0} \lt t \lt \color{#0004fc}{9}\quad \cdots\cdots \ ⑥$$
したがって,連立方程式 ② , ③ を満たす実数\( \ x \ , \ y \ \)の値は
\( \ x=\log_{3}\color{#0004fc}{\frac{ヒ}{フ}} \ , \ y=\log_{3}\color{#0004fc}{\frac{ヘ}{ホ}} \ \) であることがわかる。
$$\begin{align}t^2-11t+18=0 \ & \ \left( 0 \lt t \lt 9\right) \\\\ \left( t-2\right)\left( t-9\right)=0 \\\\ & \\\\ t=&2 \ , \ 9\\\\ 範囲より&\quad t=\color{#0004fc}{2}\end{align}$$
$$\begin{align}t=2=&\left( \frac{1}{3}\right)^x=\left( 3^{-1}\right)^x \\\\ 2=&3^{-x} \\\\ -x=&\log_{3}2\\\\ x=&-\log_{3}2\\\\ x=&\log_{3}\color{#0004fc}{\frac{1}{2}} \end{align}$$
$$\begin{align}y=&2x+1 \\\\ =&2\log_{3}\frac{1}{2}+\log_{3}3 \\\\ =&\log_{3}\left( \frac{1}{4}\times 3\right)\\\\ =&\log_{3}\color{#0004fc}{\frac{3}{4}} \end{align}$$
Lukia
そこで、ふだんの勉強では、雰囲気がわかる程度のグラフを描くようにしておくとよいと思います。
何度かやっておくと、脳内にグラフが描けるようになります。
2019年大学入試センター試験の数学の問題の一覧です。
https://makelemonadejp.com/center20191a2b/共有:
プロフィール
