高校数学の「三角比に絶対値まで絡んだ複雑な定積分」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年4月14日2023年1月14日積分とその応用実用数学技能検定（数学検定数検),数検準1級

読了時間: 約6分43秒

問題

以下の定積分を求めよ.
$$\int_{0}^{\frac{ \pi }{ 2 }} x\vert \sin^{2} x-\frac{1}{2} \vert dx$$

まずはグラフの形を定めよう。

Lukia

絶対値記号に挟まれた部分のグラフを推定したいのですが、
今回は、絶対値記号をはずす前にひと手間かけようと思います。

ディノ

そのひと手間、難しいのかぁ～～～？

Lukia

ディ、ディノさん・・・。（汗）

ディノ

まったく、みずくせぇよな。こんだけ一緒に絶対値の問題解いてきたんだから、呼べっつ～の。

Lukia

あはっ、ディノさんもお忙しいかと思いましてね。（＾◇＾；）
ま、でも、やってみてもらおうかな。
ディノさん、三角比や、三角関数は習いましたか？
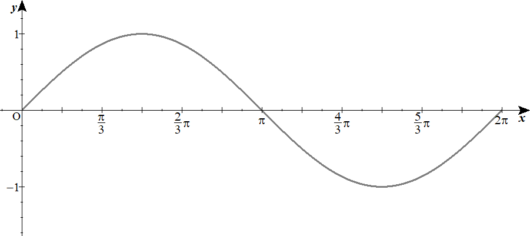
$ \ y=\sin x \ $のグラフを描いてほしいんですが。

ディノ

ってことは、アレか？
三角関数とかにもオレ、出ていいのか？

Lukia

そ、それは、おやつ代がかさむのでナシですッ！

ディノ

ふんっ、しけてんなッ。
ひとまず、$ \ y=\sin x \ $のグラフだな。
範囲は、$ \ \left( 0 \leq x \leq 2\pi\right) \ $でいいか？

Lukia

上等です。
それでは、お願いします。

ディノ

こうだな。

Lukia

いいですねぇ。
では、値域、すなわち$ \ y \ $の値の上限、下限はどうなるでしょうか。

ディノ

えっと・・・$ \ -1 \leq y \leq 1 \ $だ。

Lukia

もともと、$ \ y=\sin x \ $とおいていますから、
$ \ -1 \leq \sin x \leq 1 \ $といっても差し支えありませんね。
では、これをふまえて、今度は、$ \ y=\vert \sin^2 x-\frac{1}{2} \vert \ \left( -1 \leq \sin x \leq 1\right)$のグラフを考えていきます。

ディノ

なんか、難しそうな式になってるな。

Lukia

見かけはね。
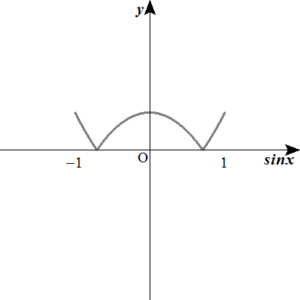
じゃ、もし、$ \ y=\vert t^2-\frac{1}{2} \vert \ \left( -1 \leq t \leq 1\right)$ならどうですか？

ディノ

なんだ、$ \ \sin x=t \ $とおくだけか。
それなら簡単だ。
こうだろ？

Lukia

はい。そのとおりです。
ちなみに、このグラフで、$ \ \sin x \ $軸と交わっているときの$ \ \sin x \ $座標はわかりますか？

ディノ

これは、$ \ \sin^2 x-\frac{1}{2}=0 \ $の解を求めるだけだから、
$ \ \sin x= \pm \frac{\sqrt{2}}{2} \ $だな。

いよいよ絶対値をはずす。

Lukia

それでは、ここで、ディノさんに描いてもらったふたつのグラフを合成しちゃいます。

ディノ

どうやるんだ？

Lukia

$ \ y=\sin x \ $のグラフを右に$ \ 90^{\circ} \ $回転させ、
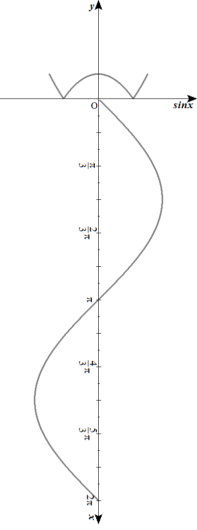
$ \ y=\vert \sin^2 x-\frac{1}{2} \vert \ $のグラフの第3象限・第4象限に重ねます。
すると、こ～なります。

ディノ

うおぉ、なんじゃこりゃ～～～！

Lukia

戸惑うかもしれませんが、まずは上のグラフを見ながら、いつも通り場合分けをしてみてください。

ディノ

えっと、まず、$ \ -1 \leq \sin x \leq -\frac{\sqrt{2}}{2} \ $のとき、
$ \ y=\sin^2 x-\frac{1}{2} \ $だ。

Lukia

そうです。いつもどおりですよ。

ディノ

じゃ、$ \ -\frac{\sqrt{2}}{2} \lt \sin x \leq \frac{\sqrt{2}}{2} \ $のとき、
$ \ y=-\sin^2 x+\frac{1}{2} \ $となる。
最後は、$ \ \frac{\sqrt{2}}{2} \lt \sin x \leq 1 \ $のとき、
$ \ y=\sin^2 x-\frac{1}{2} \ $だな。

Lukia

すばらしいです。
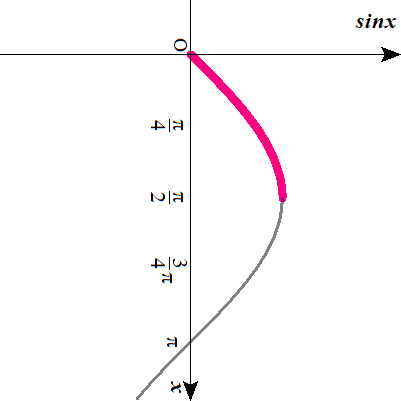
ここで、積分区間と$ \ 90^{\circ} \ $回転させた$ \ y=\sin x \ $のグラフを対応させ、
$ \ y=\vert \sin^2 x-\frac{1}{2} \vert \ $のグラフで本当に必要なところを限定していきます。

Lukia

ディノさん、今、積分区間は、$ \ 0 \ $から$ \ \frac{ \pi }{ 2 } \ $までとなっているのですが、$ \ y=\sin x \ $のグラフで対応させるなら、どうなりますか？

ディノ

下のグラフのピンクの太い曲線部分がそれにあたるよな。

Lukia

ということは、
$ \ 0 \leq \sin x \leq 1 \ $までの範囲を考えることになりますね。
上のグラフの第2象限部分は不要ということになります。

ディノ

なるほど。でも、この上のグラフは、ピンク一色でなぞることは無理だな。
もともとは放物線だが、$ \ 0 \leq \sin x \leq \frac{\sqrt{2}}{2} \ $の範囲は、上に凸の放物線だもんな。

Lukia

では、2色でなぞり分けてみてください。

ディノ

おう。こうなるな。

ディノ

つまり、$ \ 0 \leq x \leq \frac{ \pi }{ 4 } \ $のとき$ \ y=-\sin^2 x+\frac{1}{2} \ $であり、
$ \ \frac{ \pi }{ 4 } \lt x \leq \frac{ \pi }{ 2 } \ $のとき、$ \ y=\sin^2 x-\frac{1}{2} \ $となる。

Lukia

ディノさん、おつかれさまでした。
ここからは、さすがに数学Ⅲ範囲なので、私が引き取ります。
そうだ、桜餅買ってあったんですよね。
お疲れでしょう。どうぞどうぞ！（ディノさんの口に桜餅をつっこみ、追いやる）

式を立てて計算していく。

Lukia

ディノさんに大変なところをやってもらったところで、
以降は、ふきだしなしで、淡々と進めていきます。

$$\begin{align}与式=&\int_{0}^{\frac{ \pi }{ 4 }} x\left( -\sin^2 x+\frac{1}{2}\right) dx+\int_{\frac{ \pi }{ 4 }}^{\frac{ \pi }{ 2 }} x\left( \sin^2 x-\frac{1}{2}\right) dx \\\\ =&\int_{0}^{\frac{ \pi }{ 4 }} x\left( -\sin^2 x+\frac{1}{2}\right) dx-\int_{\frac{ \pi }{ 4 }}^{\frac{ \pi }{ 2 }} x\left( -\sin^2 x+\frac{1}{2}\right) dx \end{align}$$
$$\begin{align}ここで,\quad f\left( x\right)=&x\left( -\sin^2 x+\frac{1}{2}\right)\quad の原関数を\quad \mathrm{F}\left( x\right) \ とする. \\\\ 与式=&\mathrm{F}\left( \frac{ \pi }{ 4 }\right)-\mathrm{F}\left( 0\right)-\lbrace \mathrm{F}\left( \frac{ \pi }{ 2 }\right)-\mathrm{F}\left( \frac{ \pi }{ 4 }\right)\rbrace \\\\ =&2\mathrm{F}\left( \frac{ \pi }{ 4 }\right)-\mathrm{F}\left( 0\right)-\mathrm{F}\left( \frac{ \pi }{ 2 }\right) \end{align}$$

$$\begin{align}ここで,\quad &\sin^2 x=\frac{1-\cos 2x}{2}\quad より \\\\ -\sin^2 x+\frac{1}{2}=&\frac{-1+\cos 2x+1}{2}=\frac{\cos 2x}{2} \\\\ 原関数は \ \mathrm{F}\left( x\right)=&\frac{1}{4}x\sin 2x +\frac{1}{8}\cos 2x \quad である.\end{align}$$

$$\begin{align}与式=&2\left( \frac{1}{4}\times \frac{ \pi }{ 4 }\sin 2\cdot \frac{ \pi }{ 4 }+\frac{1}{8}\times 2\cdot \frac{ \pi }{ 4 }\right)-\frac{1}{8}-\left( \frac{1}{4}\times \frac{ \pi }{ 4 }\sin 2\times \frac{ \pi }{ 2 }+\frac{1}{8}\times 2\cdot \frac{ \pi }{ 2 }\right) \\\\ =&\frac{ \pi }{ 8 }\sin \frac{ \pi }{ 2 }-\frac{1}{8}+\frac{1}{8} \\\\ =&\frac{ \pi }{ 8 } \end{align}$$