高校数学の「三角比を用いた二次関数の最大・最小」に関する問題を解いてみる。（Yahoo!知恵袋より）

Lukia

\( \ \tan \theta \ \)を用いているので、一見三角比の問題のようですが、実際には、二次関数の最大値・最小値を求める問題とかわりないですね。
ということは、\( \ \tan \theta \ \)を\( \ t \ \)などの簡単な文字に置き換えてやるとイメージしやすくなると思うのですが、
やっぱり三角比の知識も必要だよね〜。と思うのが、\( \ -\frac{ \pi }{ 2 } \lt \theta \lt \frac{ \pi }{ 2 } \ \)です。
この範囲のとき、\( \ \tan \theta \ \)はどのような値を取るのかをイメージする必要がありますね。

t=tanθの値域を求める

$$\begin{align}\tan \theta=&t\quad とおくと、 \\\\ y=&t^2+2t+3\quad と表せる。 \end{align}$$
$$\begin{align}また、&-\frac{ \pi }{ 2 } \lt \theta \lt \frac{ \pi }{ 2 }\quad における \\\\ &\tan \theta\quad のグラフは以下の通り. \end{align}$$

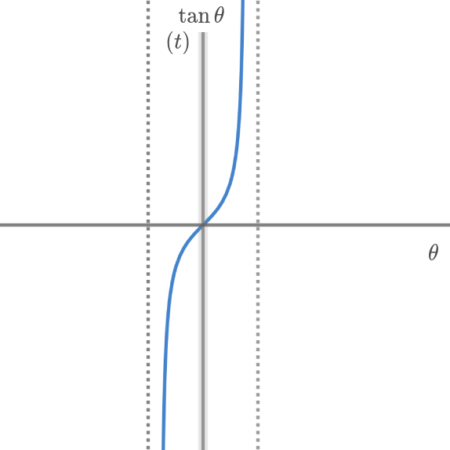
$$\begin{align}グラフより& \\\\ y=&t^2+2t+3\quad \left( t \ はすべての実数\right) \quad と表せる. \end{align}$$

Lukia

\( \ \tan \theta \ \)のグラフは、\( \ \theta=-\frac{ \pi }{ 2 } \ \),または\( \ \theta=\frac{ \pi }{ 2 } \ \)を漸近線として上下に果てしなく伸びていくグラフです。
通常、二次関数の問題で、最大・最小を考えるとき、定義域が定められていることが多いですよね。
今回の問題も、最大値・最小値を考えるのだから、定義域を決められるのではないかと思いましたが、
「ここが端っこ！」というような値を求めることはできませんでした。
よって、「\( \ t \ \)はすべての実数」というゆる〜い設定になったのです。
虚数じゃなければ、\( \ t \ \)は10000でも、0.01でも\( \ \pi \ \)や\( \ \sqrt{3} \ \)でもいいよ。ということですね。
こんなゆる〜い範囲で、はたして最大値・最小値は求められるのか。今度は、\( \ y=t^2+2t+3 \ \)のグラフを描いて考える必要がありますね。

放物線を描いて最大値・最小値を考える

$$\begin{align}y=&t^2+2t+3 \\\\ =&\left( t+1\right)^2+2 \\\\ グラフは&以下の通り. \end{align}$$

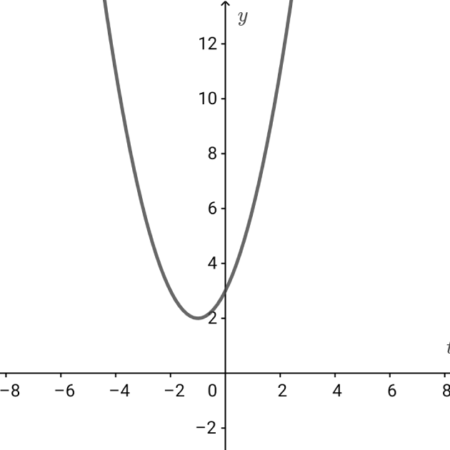
$$\begin{align}グラフ&より \\\\ t=&-1\quad のとき最小値を取る. \\\\ y=&t^2+2t+3\\\\ \quad は下に凸の関数であるため、\\\\ 最大値&を取らない.\end{align}$$

$$\begin{align}最大値& \ なし \\\\ 最小値& \\\\ 2 \ t=&-1\\\\ \quad すなわち\\\\ \tan \theta=&-1\\\\ \theta=&-\frac{ \pi }{ 4 } \end{align}$$

こたえ

$$\begin{align}最大値&\quad なし \\\\ 最小値&\quad 2\quad \left( \theta=-\frac{ \pi }{ 4 }\quad のとき\right) \end{align}$$