高校数学の「三角関数がらみの最大値・最小値」に関する問題を解いてみる。（Yahoo!知恵袋より）
[mathjax]
\(f\left( \theta\right)=3\cos 2\theta+4\sin \theta\)とする。
(1) \(\sin \theta=t\)とするとき、\(y\)を\(t\)で表せ。
(2) \(y=f\left( \theta\right)\)とおくとき、\(y\)を\(t\)で表せ。
(3) (2)の結果を利用して、\(y\)の最大値・最小値とそのときの\(t\)の値をそれぞれ求めよ。
(4) \(\alpha\)が\(0 \lt \theta \lt \frac{ \pi }{ 2 }\)を満たす角で、\(f\left( \theta\right)=3\)のとき、\(\sin \left( \alpha+\frac{ \pi }{ 6 }\right)\)を求めよ。
解法
(1)
$$\begin{align}\cos 2\theta=&1-2\sin^{2} \theta\quad より, \\\\ =&1-2t^2 \end{align}$$
(2)
$$\begin{align}y=&3\left( 1-2t^2\right)+4t \\\\ =&-6t^2+4t+3\quad \left( 0 \leq t \leq 1\right) \end{align}$$
(3)
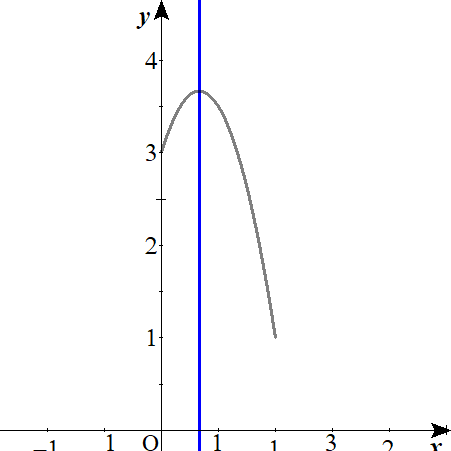
$$\begin{align}y=&g\left( t\right)\quad とする.\\\\ \ g\left( t\right)=&-6\left( t^2-\frac{2}{3}t\right)+3 \\\\ =&-6\left( t-\frac{1}{3}\right)^2+\frac{11}{3}\quad \left( 0 \leq t \leq 1\right) \end{align}$$
Lukia
上に凸の関数ですので、頂点で最大値、軸の\(t=\frac{1}{3}\)からより離れた\(t=1\)のときに最小値を取ります。
$$\begin{align}最大値\quad \frac{11}{3}\quad \quad t=\frac{1}{3} \ のとき \\\\最小値\quad 1\quad \quad t=1 \ のとき\end{align}$$
(4)
$$\begin{align}f\left( \alpha\right)=g\left( t\right)=-6t^2+4t+3=&\color{red}{3} \\\\ -6t^2+4t=&0 \\\\ t\left( -6t+4\right)=&0\\\\ t=0 \ , \ t=&\frac{2}{3} \end{align}$$
$$\begin{align}ただし\quad 0 \lt &\theta \lt \frac{ \pi }{ 2 } \\\\ 0 \lt &\sin \theta=t \lt 1\quad より, \\\\ t=&\frac{2}{3} \end{align}$$
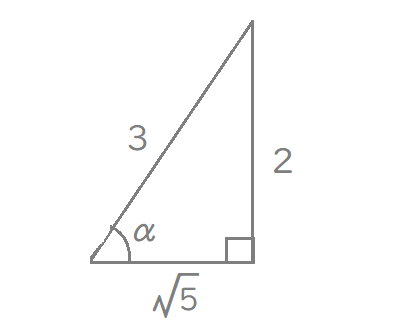
$$\begin{align}t=\sin \alpha=&\frac{2}{3}\quad より, \\\\ \cos \alpha=&\frac{\sqrt{5}}{3} \end{align}$$
$$\begin{align}\sin \left( \alpha+\frac{ \pi }{ 6 }\right)=&\sin \alpha\cdot \cos \frac{ \pi }{ 6 }+\cos \alpha\cdot \sin \frac{ \pi }{ 6 } \\\\ =&\frac{2}{3}\cdot \frac{\sqrt{3}}{2}+\frac{\sqrt{5}}{3}\cdot \frac{1}{2}\\\\ =&\frac{2\sqrt{3}+\sqrt{5}}{6} \end{align}$$
こたえ
$$\begin{align}\left( 1\right)& \\\\ &\cos 2\theta=1-2t^2 \\\\ \left( 2\right)&\\\\ &y=-6t^2+4t+3\quad \left( 0 \leq t \leq 1\right) \ \\\\ \left( 3\right)&\\\\&最大値\quad \frac{11}{3}\quad \quad t=\frac{1}{3} \ のとき \\\\&最小値\quad 1\quad \quad t=1 \ のとき\\\\ \left( 4\right)& \\\\&\sin \left( \alpha+\frac{ \pi }{ 6 }\right)=\frac{2\sqrt{3}+\sqrt{5}}{6} \end{align}$$
共有:
プロフィール
