高校数学の「空間ベクトルと内分比・一直線上に3点が存在すること」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年12月6日2023年1月14日ベクトル実用数学技能検定（数学検定数検),数検2級,数検準1級

読了時間: 約7分25秒

[mathjax]

問題

四面体$\mathrm{OABC}$において、辺$\mathrm{OA}$を$4:3$に内分する点を$\mathrm{P}$、辺$\mathrm{BC}$を$5:3$に内分する点を$\mathrm{Q}$、線分$\mathrm{PQ}$の中点を$\mathrm{M}$とする。
$\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{a}} \ , \ \overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{b}} \ , \ \overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{c}}$とするとき、次の問に答えよ。
(1)$\overrightarrow{\mathrm{OQ}}$を$\overrightarrow{\mathrm{b}} \ , \ \overrightarrow{\mathrm{c}}$を用いて表せ。また、$\overrightarrow{\mathrm{OM}}$を$\overrightarrow{\mathrm{a}} \ , \ \overrightarrow{\mathrm{b}} \ , \ \overrightarrow{\mathrm{c}}$を用いて表せ。
(2)$\overrightarrow{\mathrm{AN}}=t\overrightarrow{\mathrm{AM}}$（$t$は実数）となる点$\mathrm{N}$をとるとき、$\overrightarrow{\mathrm{ON}}$を$t \ , \ \overrightarrow{\mathrm{a}} \ , \ \overrightarrow{\mathrm{b}} \ , \ \overrightarrow{\mathrm{c}}$を用いて表せ。
(3)(2)の点$\mathrm{N}$が平面$\mathrm{OBC}$上にあるとき、$t$の値を求めよ。
またこのとき、3点$\mathrm{O} \ , \ \mathrm{N} \ , \ \mathrm{Q}$は一直線上にあることを示せ。

空間図形を描いて、情報を書き込んでみる。

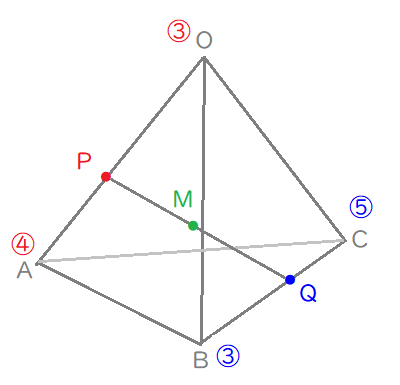
Lukia

いつものように、簡単な空間図形を描きます。そして、わかっていること、今回ですと内分比や内分点ですね。それらの情報を書き込んでいきます。
点$\mathrm{M}$が線分$\mathrm{PQ}$を$1:1$に内分することで、全体の内分比が統一できますね。
（かなりすごい数になりますが気にしない・・・）

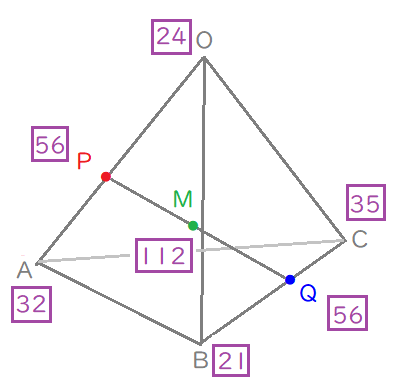
$$\begin{align}\overrightarrow{\mathrm{OQ}}=&\frac{1}{8}\left( 3\overrightarrow{\mathrm{b}}+5\overrightarrow{\mathrm{c}}\right) \\\\ \overrightarrow{\mathrm{OM}}=&\frac{1}{112}\left( 32\overrightarrow{\mathrm{a}}+21\overrightarrow{\mathrm{b}}+35\overrightarrow{\mathrm{c}}\right) \end{align}$$

Lukia

内分比を統一してしまうと、頂点にある数字を読み取っていけばいいだけなので、楽に解けますね。

式変形をしてベクトルONを求める。

$$\begin{align}\overrightarrow{\mathrm{AN}}=&t\overrightarrow{\mathrm{AM}} \\\\ \overrightarrow{\mathrm{ON}}-\overrightarrow{\mathrm{a}}=&t\left( \overrightarrow{\mathrm{OM}}-\overrightarrow{\mathrm{a}}\right) \\\\ \overrightarrow{\mathrm{ON}}=&t\overrightarrow{\mathrm{OM}}-t\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{a}}\\\\ =&\frac{1}{112}\left( 112-80t\right)+\frac{t}{112}\left( 21\overrightarrow{\mathrm{b}}+35\overrightarrow{\mathrm{c}}\right)\\\\ =&\frac{1}{7}\left( 7-5t\right)\overrightarrow{\mathrm{a}}+\frac{t}{16}\left( 3\overrightarrow{\mathrm{b}}+5\overrightarrow{\mathrm{c}}\right) \end{align}$$

内分比の統一は煩雑な解法のみちしるべとなる。

Lukia

点$\mathrm{N}$が平面$\mathrm{OBC}$上にあるということは、
$\overrightarrow{\mathrm{ON}}=l\overrightarrow{\mathrm{b}}+m\overrightarrow{\mathrm{c}}$とあらわせることになります。

Lukia

また、$\overrightarrow{\mathrm{AN}}=t\overrightarrow{\mathrm{AM}}$より、点$\mathrm{M}$は線分$\mathrm{AN}$の内分点だということがいえますね。

Lukia

ちょっとずるいのですが、問題から、点$\mathrm{N}$は線分$\mathrm{OQ}$を内分すると読み取れるので、それを使って、あらかじめ確かめてしまいます。

Lukia

内分比の計算からも、すでに点$\mathrm{N}$が線分$\mathrm{OQ}$の内分点であり、3点$\mathrm{O} \ , \ \mathrm{N} \ , \ \mathrm{Q}$が一直線上に並んでいることがわかりますね。
しかし、これは証明にはなりませんので、のちほど実際に計算して間違いないことを確かめていきましょう。

$$\begin{align}\overrightarrow{\mathrm{AN}}=&t\overrightarrow{\mathrm{AM}} \ より\\\\ 点\mathrm{M}は線分&\mathrm{AN}の内分点であることがわかる。\\\\ \overrightarrow{\mathrm{AM}}=&\frac{5}{7}\overrightarrow{\mathrm{AN}} \\\\すなわち\quad \overrightarrow{\mathrm{AN}}=&\frac{7}{5}\overrightarrow{\mathrm{AM}} \ より\\\\ \\\\ t=&\frac{7}{5} \end{align}$$

$$\begin{align}\overrightarrow{\mathrm{OQ}}=&k\overrightarrow{\mathrm{ON}} \ を満たす実数 \ k \ \left( k \neq 0\right) \ を求める。\\\\ \\\\ \overrightarrow{\mathrm{AN}}=&\frac{7}{5}\overrightarrow{\mathrm{AM}} \\\\ 5\overrightarrow{\mathrm{ON}}-5\overrightarrow{\mathrm{a}}=&7\overrightarrow{\mathrm{OM}}-7\overrightarrow{\mathrm{a}}\\\\ 5\overrightarrow{\mathrm{ON}}=&7\overrightarrow{\mathrm{OM}}-2\overrightarrow{\mathrm{a}}\\\\ =&\frac{7}{112}\left( 32\overrightarrow{\mathrm{a}}+21\overrightarrow{\mathrm{b}}+35\overrightarrow{\mathrm{c}}\right)-2\overrightarrow{\mathrm{a}}\\\\ 5\overrightarrow{\mathrm{ON}}=&\frac{7}{16}\left( 3\overrightarrow{\mathrm{b}}+5\overrightarrow{\mathrm{c}}\right)\\\\ \overrightarrow{\mathrm{ON}}=&\frac{7}{80}\left( 3\overrightarrow{\mathrm{b}}+5\overrightarrow{\mathrm{c}}\right) \end{align}$$
仮定より、
$$\begin{align}\overrightarrow{\mathrm{OQ}}=&k\overrightarrow{\mathrm{ON}} \\\\ \frac{1}{8}\left( 3\overrightarrow{\mathrm{b}}+5\overrightarrow{\mathrm{c}}\right)=&k\cdot \frac{7}{80}\left( 3\overrightarrow{\mathrm{b}}+5\overrightarrow{\mathrm{c}}\right) \\\\ \\\\ k=&\frac{10}{7}\\\\ \\\\ 以上より \ &\overrightarrow{\mathrm{OQ}} =\frac{10}{7}\overrightarrow{\mathrm{ON}} \ を満たすので,\\\\ &3点 \ \mathrm{O} \ , \ \mathrm{N} \ ,\mathrm{Q} \ は一直線上にあるといえる。 \end{align}$$

こたえ

$$\begin{align}\left( 1\right)& \\\\& \overrightarrow{\mathrm{OQ}}=\frac{1}{8}\left( 3\overrightarrow{\mathrm{b}}+5\overrightarrow{\mathrm{c}}\right) \\\\ & \overrightarrow{\mathrm{OM}}=\frac{1}{112}\left( 32\overrightarrow{\mathrm{a}}+21\overrightarrow{\mathrm{b}}+35\overrightarrow{\mathrm{c}}\right)\\\\ \left( 2\right)&\\\\ &\overrightarrow{\mathrm{ON}}=\frac{1}{7}\left( 7-5t\right)\overrightarrow{\mathrm{a}}+\frac{t}{16}\left( 3\overrightarrow{\mathrm{b}}+5\overrightarrow{\mathrm{c}}\right)\\\\ \\\\\left( 3\right)&\\\\ &t=\frac{7}{5}\\\\ &証明は省略 \end{align}$$