高校数学の「三角不等式（タンジェント）」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年11月16日2023年1月14日三角関数実用数学技能検定（数学検定 数検),数検2級,数検準1級

[mathjax]

$$\begin{align}0 \leq \theta \lt 2\pi \ において \\\\ \tan \theta=1 \ となるのは \\\\ \theta=\frac{ \pi }{ 4 } \ , \ または \ \theta={\frac{ 5 }{ 4 }}\pi \end{align}$$

Lukia

ここで、\(\tan \theta\)のグラフを思い出してほしいのですが、
\(\theta\)が\(0\)から\(\frac{ \pi }{ 2 }\)に近づくにつれ、\(\tan \theta\)の値は無限大に大きくなり、
\(\theta\)が\(\pi\)から\({\frac{ 3 }{ 2 }}\pi\)に近づくにつれ、\(\tan \theta\)の値は無限大に小さくなっていきます。
そのほか、第二象限と第四象限は、ともに負ですから、不等式を満たしていますね。

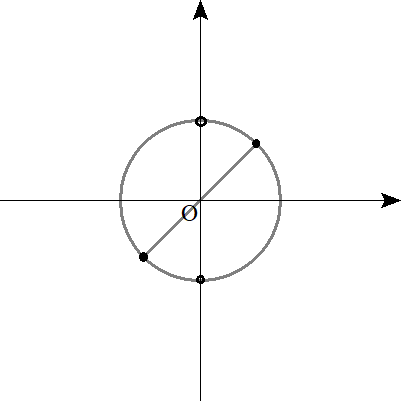
ゆえに、
$$\begin{align}0 \leq &\theta \leq \frac{ \pi }{ 4 }, \\\\ \frac{ \pi }{ 2 } \lt &\theta \leq {\frac{ 5 }{ 4 }}\pi, \\\\ {\frac{ 3 }{ 2 }}\pi \lt &\theta \lt 2\pi \end{align}$$

こたえ

$$\begin{align}0 \leq &\theta \leq \frac{ \pi }{ 4 } ,\\\\ \frac{ \pi }{ 2 } \lt &\theta \leq {\frac{ 5 }{ 4 }}\pi, \\\\ {\frac{ 3 }{ 2 }}\pi \lt &\theta \lt 2\pi \end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。