高校数学の「定義域の両端が動く関数の最大・最小（難しい）」に関する問題を解いてみる。(Yahoo!知恵袋より)
読了時間: 約6分0秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「定義域の両端が動く関数の最大・最小（難しい）」に関する問題を解いてみました。もし、この記事の問題が難しいようなら、もう少しやさしめの問題があります。
まずは、こちらからどうぞ。
https://makelemonadejp.com/yc-236
問題
\( \ t \leq x \leq t+1 \ \)における
関数 \( \ y=\left( \vert x-4 \vert-1\right)^2 \ \)の
最大値を\( \ f\left( t\right) \ \)とするとき、\( \ f\left( t\right) \ \)を求めよ。
関数 \( \ y=\left( \vert x-4 \vert-1\right)^2 \ \)の
最大値を\( \ f\left( t\right) \ \)とするとき、\( \ f\left( t\right) \ \)を求めよ。
解法
与えられた関数を以下のようにおく。
$$\begin{align}h\left( x\right)=&\left( x-5\right)^2\quad x \geq 4 \ のとき \\\\ g\left( x\right)=&\left( x-3\right)^2\quad x \lt 4 \ のとき \end{align}$$ また、定義域の中央 \( \ x=\frac{2t+1}{2} \ \) を「軸」とする。
(1)
定義域の右端が\( \ g\left( x\right) \ \)の軸よりも左にあるとき
$$\begin{align}t+1\lt &3\quad すなわち \\\\ t \lt &2 \quad のとき \\\\ f\left( t\right)=&g\left( t\right)=\left( t-3\right)^2 \end{align}$$
(2)
\( \ g\left( x\right) \ \) の軸が 定義域の「軸」と定義域の右端の間にあるとき
$$\begin{align}\frac{2t+1}{2} \lt &3 \lt t+1\quad すなわち \\\\ 2 \lt &t \lt \frac{5}{2} \ のとき \\\\ f\left( t\right)=&\left( t-3\right)^2 \end{align}$$
(3)
定義域の「軸」と\( \ g\left( x\right) \ \)の軸が重なるとき
$$\begin{align}\frac{2t+1}{2}=&3\quad すなわち \\\\ t=&\frac{5}{2}\quad のとき \\\\ f\left( t\right)=g\left( \frac{5}{2}\right)=g\left( \frac{7}{2}\right)=&\frac{1}{4} \end{align}$$
(4)
\( \ g\left( x\right) \ \)の軸が、定義域の左端と「軸」の間にあるとき
$$\begin{align}3 \lt \frac{2t+1}{2} \lt& \frac{7}{2}\quad すなわち \\\\ \frac{5}{2} \lt &t \lt 3\quad のとき \\\\ f\left( t\right)=&g\left( t+1\right)^2=\left( t-2\right)^2 \end{align}$$
(5)
定義域の右端が\( \ x=4 \ \) 上にあるとき
定義域の左端が\( \ g\left( x\right) \ \) の軸に重なるので、
$$\begin{align}t=&3\quad のとき \\\\ f\left( t\right)=&g\left( 4\right)=1 \end{align}$$
(6)
定義域の右端が\( \ h\left( x\right) \ \) の軸の左側にあるとき
$$\begin{align}3 \leq t \lt &4\quad のとき \\\\ f\left( t\right)=&g\left( 4\right)=h\left( 4\right)=1 \end{align}$$
(7)
定義域の右端が\( \ h\left( x\right) \ \) の軸と重なるとき
$$\begin{align} t=&4\quad のとき \\\\ f\left( t\right)=&h\left( 4\right)=1 \end{align}$$
(8)
\( \ h\left( x\right) \ \) の軸が定義域の「軸」と定義域の右端の間にあるとき
$$\begin{align}\frac{2t+1}{2} \lt &5 \lt t+1\quad すなわち \\\\ 4 \lt &t \lt \frac{5}{2}\quad のとき \\\\ f\left( t\right)=&h\left( t\right)=\left( t-5\right)^2 \end{align}$$
(9)
定義域の「軸」と\( \ h\left( x\right) \ \)の軸が重なるとき
$$\begin{align}t=&\frac{9}{2}\quad のとき \\\\ f\left( t\right)=&h\left( \frac{9}{2}\right)=h\left( \frac{11}{2}\right)=\frac{1}{4} \end{align}$$
(10)
\( \ h\left( x\right) \ \) の軸が定義域の左端と定義域の「軸」の間にあるとき
$$\begin{align}t \lt 5 \lt &\frac{2t+1}{2}\quad すなわち \\\\ \frac{9}{2} \lt &t \lt 5\quad のとき \\\\ f\left( t\right)=&h\left( t+1\right)=\left( t-4\right)^2 \end{align}$$
(11)
定義域の左端が\( \ h\left( x\right) \ \)の軸と重なるとき
$$\begin{align}t=&5\quad のとき \\\\ f\left( t\right)=&\left( t-4\right)^2 \end{align}$$
(12)
定義域の左端が \( \ h\left( x\right) \ \) の軸よりも右側にあるとき
$$\begin{align}5 \lt &t\quad のとき \\\\ f\left( t\right)=&h\left( t+1\right)=\left( t-4\right)^2 \end{align}$$
$$\begin{align} f\left( t\right)=&\left( t-3\right)^2\quad t \lt \frac{5}{2} \ のとき \\\\ f\left( t\right)=&\frac{1}{4}\quad t=\frac{5}{2} \ のとき \\\\ f\left( t\right)=&\left( t-2\right)^2\quad \frac{5}{2} \lt t \lt 3 \ のとき\\\\ f\left( t\right)=&1\quad 3 \leq t \leq 4 \ のとき\\\\ f\left( t\right)=&\left( t-5\right)^2\quad 4 \lt t \lt \frac{9}{2} \ のとき\\\\ f\left( t\right)=&\frac{1}{4}\quad t=\frac{9}{2} \ のとき \\\\ f\left( t\right)=&\left( t-4\right)^2\quad \frac{9}{2} \lt t \ のとき \end{align}$$
$$\begin{align}h\left( x\right)=&\left( x-5\right)^2\quad x \geq 4 \ のとき \\\\ g\left( x\right)=&\left( x-3\right)^2\quad x \lt 4 \ のとき \end{align}$$ また、定義域の中央 \( \ x=\frac{2t+1}{2} \ \) を「軸」とする。
(1)
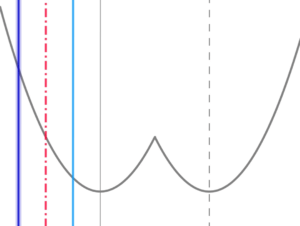定義域の右端が\( \ g\left( x\right) \ \)の軸よりも左にあるとき$$\begin{align}t+1\lt &3\quad すなわち \\\\ t \lt &2 \quad のとき \\\\ f\left( t\right)=&g\left( t\right)=\left( t-3\right)^2 \end{align}$$
(2)
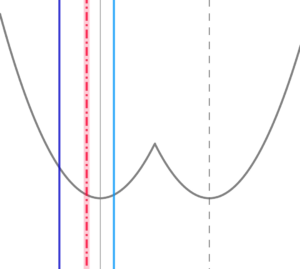\( \ g\left( x\right) \ \) の軸が 定義域の「軸」と定義域の右端の間にあるとき$$\begin{align}\frac{2t+1}{2} \lt &3 \lt t+1\quad すなわち \\\\ 2 \lt &t \lt \frac{5}{2} \ のとき \\\\ f\left( t\right)=&\left( t-3\right)^2 \end{align}$$
(3)
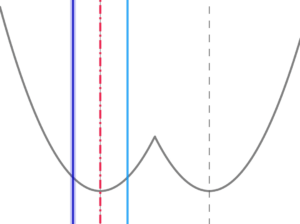定義域の「軸」と\( \ g\left( x\right) \ \)の軸が重なるとき$$\begin{align}\frac{2t+1}{2}=&3\quad すなわち \\\\ t=&\frac{5}{2}\quad のとき \\\\ f\left( t\right)=g\left( \frac{5}{2}\right)=g\left( \frac{7}{2}\right)=&\frac{1}{4} \end{align}$$
(4)
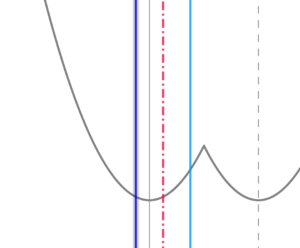\( \ g\left( x\right) \ \)の軸が、定義域の左端と「軸」の間にあるとき$$\begin{align}3 \lt \frac{2t+1}{2} \lt& \frac{7}{2}\quad すなわち \\\\ \frac{5}{2} \lt &t \lt 3\quad のとき \\\\ f\left( t\right)=&g\left( t+1\right)^2=\left( t-2\right)^2 \end{align}$$
(5)
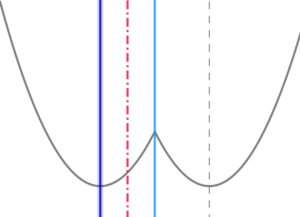定義域の右端が\( \ x=4 \ \) 上にあるとき定義域の左端が\( \ g\left( x\right) \ \) の軸に重なるので、
$$\begin{align}t=&3\quad のとき \\\\ f\left( t\right)=&g\left( 4\right)=1 \end{align}$$
(6)
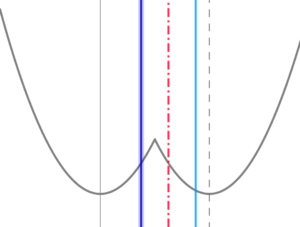定義域の右端が\( \ h\left( x\right) \ \) の軸の左側にあるとき$$\begin{align}3 \leq t \lt &4\quad のとき \\\\ f\left( t\right)=&g\left( 4\right)=h\left( 4\right)=1 \end{align}$$
(7)
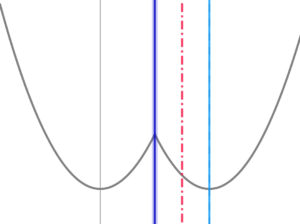定義域の右端が\( \ h\left( x\right) \ \) の軸と重なるとき$$\begin{align} t=&4\quad のとき \\\\ f\left( t\right)=&h\left( 4\right)=1 \end{align}$$
(8)
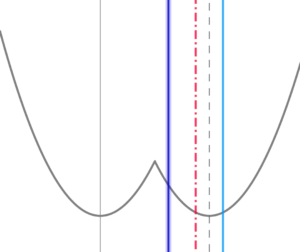\( \ h\left( x\right) \ \) の軸が定義域の「軸」と定義域の右端の間にあるとき$$\begin{align}\frac{2t+1}{2} \lt &5 \lt t+1\quad すなわち \\\\ 4 \lt &t \lt \frac{5}{2}\quad のとき \\\\ f\left( t\right)=&h\left( t\right)=\left( t-5\right)^2 \end{align}$$
(9)
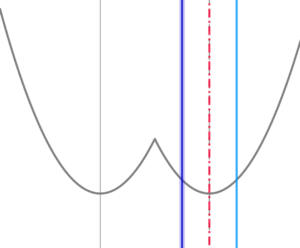定義域の「軸」と\( \ h\left( x\right) \ \)の軸が重なるとき$$\begin{align}t=&\frac{9}{2}\quad のとき \\\\ f\left( t\right)=&h\left( \frac{9}{2}\right)=h\left( \frac{11}{2}\right)=\frac{1}{4} \end{align}$$
(10)
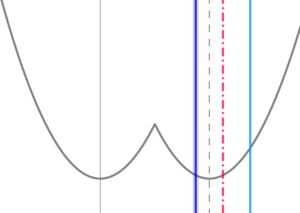\( \ h\left( x\right) \ \) の軸が定義域の左端と定義域の「軸」の間にあるとき$$\begin{align}t \lt 5 \lt &\frac{2t+1}{2}\quad すなわち \\\\ \frac{9}{2} \lt &t \lt 5\quad のとき \\\\ f\left( t\right)=&h\left( t+1\right)=\left( t-4\right)^2 \end{align}$$
(11)
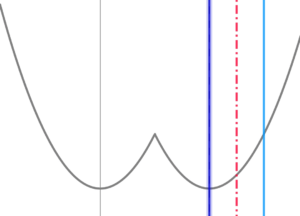定義域の左端が\( \ h\left( x\right) \ \)の軸と重なるとき$$\begin{align}t=&5\quad のとき \\\\ f\left( t\right)=&\left( t-4\right)^2 \end{align}$$
(12)
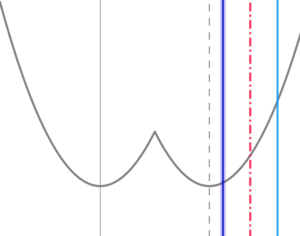定義域の左端が \( \ h\left( x\right) \ \) の軸よりも右側にあるときまとめ
以上より$$\begin{align}5 \lt &t\quad のとき \\\\ f\left( t\right)=&h\left( t+1\right)=\left( t-4\right)^2 \end{align}$$
12通りも場合分けして、ヘトヘトです。。。
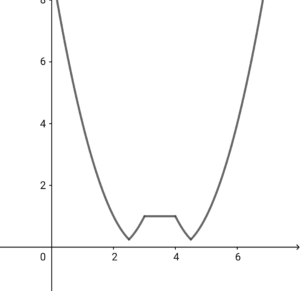
ちなみに、上記のまとめをグラフにしてみると、以下の図のようになりました。
なんか、逆さまのにゃんこしゃんに見えます。(笑)
関数でもお絵かきできるって素敵！
ちなみに、上記のまとめをグラフにしてみると、以下の図のようになりました。
なんか、逆さまのにゃんこしゃんに見えます。(笑)
関数でもお絵かきできるって素敵！
こたえ
$$\begin{align} f\left( t\right)=&\left( t-3\right)^2\quad t \lt \frac{5}{2} \ のとき \\\\ f\left( t\right)=&\frac{1}{4}\quad t=\frac{5}{2} \ のとき \\\\ f\left( t\right)=&\left( t-2\right)^2\quad \frac{5}{2} \lt t \lt 3 \ のとき\\\\ f\left( t\right)=&1\quad 3 \leq t \leq 4 \ のとき\\\\ f\left( t\right)=&\left( t-5\right)^2\quad 4 \lt t \lt \frac{9}{2} \ のとき\\\\ f\left( t\right)=&\frac{1}{4}\quad t=\frac{9}{2} \ のとき \\\\ f\left( t\right)=&\left( t-4\right)^2\quad \frac{9}{2} \lt t \ のとき \end{align}$$共有:
プロフィール
Author Profile