高校数学の「放物線(二次関数)の最小値」に関する問題を解いてみる。(Yahoo!知恵袋より)

[mathjax]
ただし, \( \ a \ \)は実数の定数とする.
(1) \( \ y \ \)の最小値が\( \ -4 \ \)のとき,\( \ a \ \)の値を求めよ.
(2) \( \ -1 \leq x \leq 4 \ \)における最小値が\( \ -4 \ \)となるような\( \ a \ \)の値をすべて求めよ.
(3) \( \ a \leq x \leq a+1 \ \)における\( \ y \ \)の最小値を\( \ m\left( a\right) \ \)とおくとき,\( \ m\left( a\right) \ \)を\( \ a \ \)を用いて表せ.さらに,関数\( \ y=m\left( a\right) \ \)のグラフをかけ.
放物線の凸の方向を確認する習慣をつけよう。

Lukia
さらに(1)では、定義域(\( \ x \ \)の値が取る範囲)が特に定められていないので、頂点が最小値であることがわかります。
$$\begin{align}y=x^2-ax=&\left( x-\frac{a}{2}\right)^2-\frac{a^2}{4}\quad より, \\\\ -\frac{a^2}{4}=&-4 \\\\ a^2=&16\\\\ a=& \pm 4 \end{align}$$
定義域が固定されているなら「軸の位置」で場合分けをする。

Lukia
(放物線,二次関数が出てきたら、必ず軸と頂点を求めておきましょう。)

Lukia
下に凸の放物線であっても、頂点が最小値とは限らない。ということになってしまいます。
そこで、「軸の位置」を場合分けすることによって、最小値を取る\( \ x \ \)の値を絞り込んでいきます。

Lukia
\( \ x \ \)軸と交わるのは、\( \ x=0 \ , \ x=a \ \)とわかっています。
しかし、問題では、「\( \ a \ \)は実数。」と定められているだけなので、正かもしれない、負かもしれない、なんならゼロかもしれないのです。
というわけで、まずは、ざっくりと\( \ a \ \)が正のとき、負のとき、ゼロのとき。と場合分けをして、さらに細かく定義域内の「軸の位置」を考えていきます。
$$以下,\quad y=f\left( x\right)\quad とする.$$
$$Ⅰ)\quad a \gt 0 \ のとき$$
$$ⅰ)\quad 4 \lt \frac{a}{2}\quad のとき$$


Lukia
最小値は,図中の青い点が示す\( \ f\left( 4\right) \ \)となります。
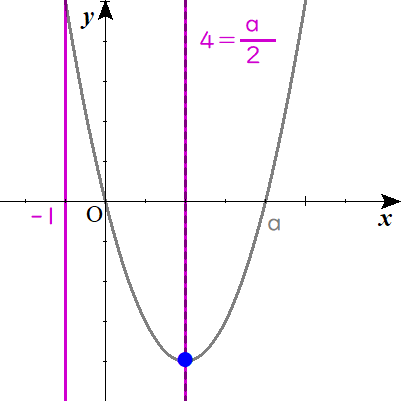
$$ⅱ)\quad 4 =\frac{a}{2}\quad のとき$$

Lukia
すると、軸と定義域の右端が重なったときまでは、\( \ f\left( 4\right) \ \)が最小値となることがわかりますね。
この二つの図の状態をまとめてみます。
$$\begin{align}4 \leq &\frac{a}{2} \quad すなわち \ 8 \leq a \ のとき\\\\ f\left( 4\right)=&16-4a=-4 \\\\ a=&5\\\\ 8 \leq &a\quad を満たさないので不適. \end{align}$$
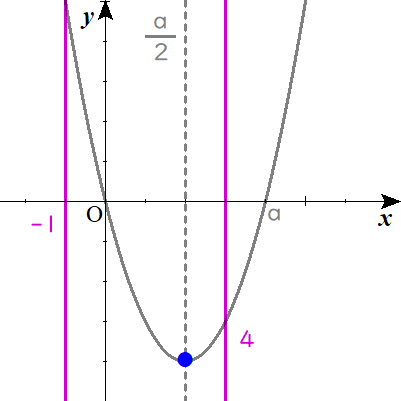
$$ⅲ)\quad \frac{a}{2} \lt 4\quad のとき$$

Lukia
この場合は、頂点が定義域に含まれているわけですから、\( \ f\left( \frac{a}{2}\right) \ \)が最小値だといえますね。
$$\begin{align}\frac{a}{2} \lt &4\quad すなわち \ a \lt 8 \ のとき \\\\ f\left( \frac{a}{2}\right)=&-\frac{a^2}{4}=-4 \\\\ a^2=&16\\\\ 0 \lt &a \lt 8\quad より\\\\ a=&4 \end{align}$$
$$Ⅱ)\quad a = 0 \ のとき$$
$$\begin{align}y=&x^2 \\\\ &最小値は \ 0 \ であるので,不適.\end{align}$$

Lukia
$$Ⅲ)\quad a \lt 0 \ のとき$$

Lukia
$$ⅰ)\quad -1 \leq \frac{a}{2}\quad のとき$$
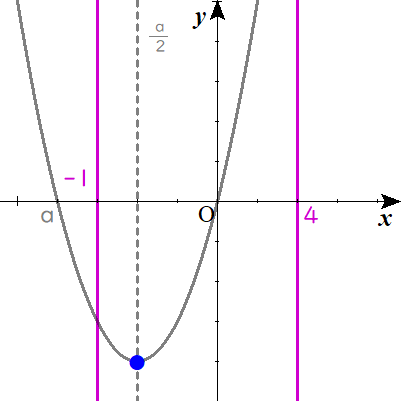
$$\begin{align}-1 \leq &\frac{a}{2}\quad すなわち\quad -2 \leq a \ のとき \\\\ f\left( \frac{a}{2}\right)=&-\frac{a^2}{4}=-4 \\\\ a^2=&16\\\\ a=& \pm 4\\\\ &どちらも \ -2 \leq a \lt 0 \ を満たさないので, \ 不適. \end{align}$$
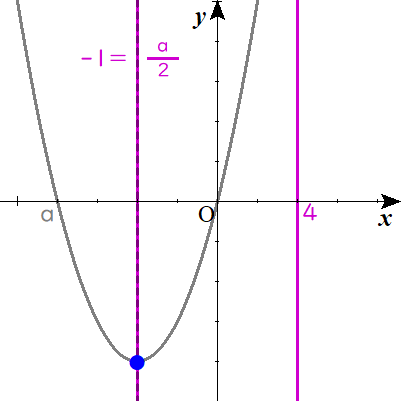
$$ⅱ)\quad -1 \gt \frac{a}{2}\quad のとき$$
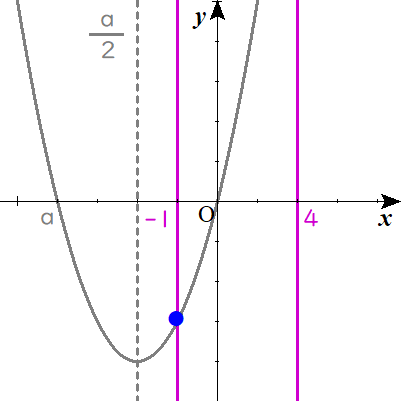
$$\begin{align}\frac{a}{2} \lt &-1\quad すなわち \ a \lt -2 \ のとき \\\\ f\left( -1\right)=&1+a=-4 \\\\ a=&-5 \end{align}$$
$$Ⅰ, \ Ⅱ \ より\quad a=4 \ , \ -5$$
じ、自由すぎる・・・

Lukia
こういうときは、機械的に放物線を5つ描き、軸と定義域を描き込んでいくに限ります。
$$ⅰ)\quad a+1 \lt \frac{a}{2} \ のとき$$
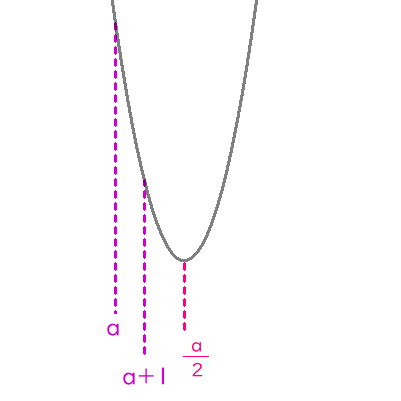
$$\begin{align}a+1 \lt &\frac{a}{2}\quad すなわち \ a \lt -2 \ のとき \\\\ m\left( a\right)=&f\left( a+1\right)=a+1 \end{align}$$
$$ⅱ)\quad a \leq \frac{a}{2} \leq a+1 \ のとき$$

$$\begin{align}a \leq &\frac{a}{2} \leq a+1\quad すなわち-2 \leq a \leq 0\quad のとき \\\\ m\left( a\right)=&f\left( \frac{a}{2}\right) =-\frac{a^2}{4} \end{align}$$
$$ⅲ)\quad \frac{a}{2} \lt a \ のとき$$
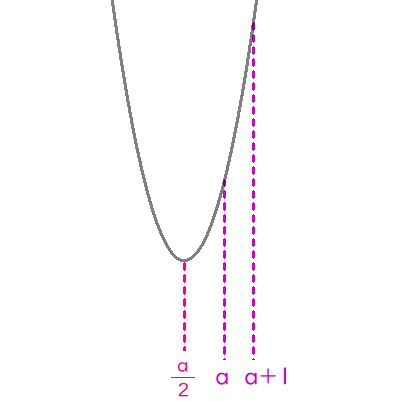
$$\begin{align} \frac{a}{2} \lt &a\quad すなわち \ 0 \lt a \ のとき \\\\ m\left( a\right)=&f\left( a\right)=0 \end{align}$$
グラフは以下の通り.
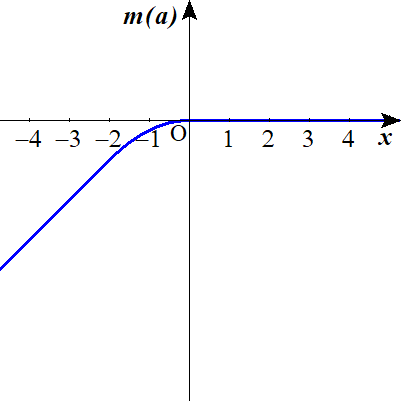
[subscribe2]









ディスカッション
コメント一覧
まだ、コメントがありません