高校数学の「定義域の両端が動く関数の最大・最小（やさしめ）」に関する問題を解いてみる。(Yahoo!知恵袋より)
読了時間: 約3分26秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「定義域の両端が動く関数の最大・最小（やさしめ）」に関する問題を解いてみました。
問題
\( \ a \ \)は定数とする。関数\( \ y=x^2-2x+1 \ \) \( \ \left( a \leq x \leq a+1\right) \ \)について、次の問に答えよ。
(1) 最小値を求めよ。
(2) 最大値を求めよ。
(1) 最小値を求めよ。
(2) 最大値を求めよ。
解法
定義域が移動する場合も、定義域の「軸」と放物線の軸との位置関係を意識することが大切です。
以下、５つのグラフを載せますが、線の色分けをしています。
灰色の点線：放物線の軸
赤い実線：定義域の右端→\( \ f\left( a+1\right) \ \) と表せる
紫の実線：定義域の中央（今回は、「軸」と表すことにします）
→ \(\Large f\left( \frac{2a+1}{2}\right)\) と表せる
青の実線：定義域の左端→\( \ f\left( a\right) \ \)
以下、５つのグラフを載せますが、線の色分けをしています。
灰色の点線：放物線の軸
赤い実線：定義域の右端→\( \ f\left( a+1\right) \ \) と表せる
紫の実線：定義域の中央（今回は、「軸」と表すことにします）
→ \(\Large f\left( \frac{2a+1}{2}\right)\) と表せる
青の実線：定義域の左端→\( \ f\left( a\right) \ \)
定義域の右端が軸よりも左にあるとき
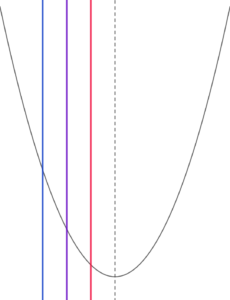
定義域の右端が放物線の軸よりも左側にある場合、
すなわち、 \( \ a+1 \lt 1 \ \)
整理して \( \ a \lt 0 \ \) のとき
最小値：\( \ f\left( a+1\right)=a^2 \ \)
最大値：\( \ f\left( a\right)=\left( a-1\right)^2 \ \)
すなわち、 \( \ a+1 \lt 1 \ \)
整理して \( \ a \lt 0 \ \) のとき
最小値：\( \ f\left( a+1\right)=a^2 \ \)
最大値：\( \ f\left( a\right)=\left( a-1\right)^2 \ \)
放物線の軸が定義域の右端と定義域の「軸」の間にあるとき
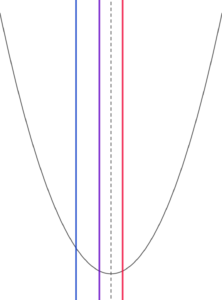
放物線の軸が定義域の右端と定義域の「軸」の間にある場合、
すなわち、 \( \ \frac{2a+1}{2} \lt 1 \leq a+1 \ \)
整理して \( \ 0 \leq a \lt \frac{1}{2} \ \) のとき
最小値：\( \ f\left( 1\right)=0 \ \)
最大値：\( \ f\left( a\right)=\left( a-1\right)^2 \ \)
すなわち、 \( \ \frac{2a+1}{2} \lt 1 \leq a+1 \ \)
整理して \( \ 0 \leq a \lt \frac{1}{2} \ \) のとき
最小値：\( \ f\left( 1\right)=0 \ \)
最大値：\( \ f\left( a\right)=\left( a-1\right)^2 \ \)
定義域の「軸」と放物線の軸が重なるとき
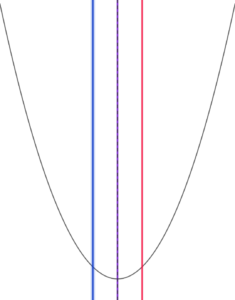
定義域の「軸」と放物線の軸が重なる場合、
すなわち、 \( \ \frac{2a+1}{2}=1 \ \)
整理して \( \ a=\frac{1}{2} \ \) のとき
最小値：\( \ f\left( 1\right)=0 \ \)
最大値：\( \ f\left( \frac{1}{2}\right)=f\left( \frac{3}{2}\right)=\frac{1}{4} \ \)
放物線の軸が定義域の左端と定義域の「軸」の間にあるとき
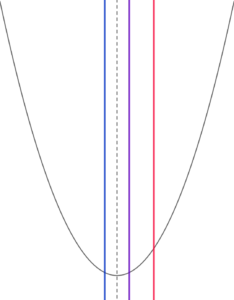
放物線の軸が定義域の左端と定義域の「軸」の間にある場合、
すなわち、 \( \ a \leq 1 \lt \frac{2a+1}{2} \ \)
整理して \( \ \frac{1}{2} \lt a \leq 1 \ \) のとき
最小値：\( \ f\left( 1\right)=0 \ \)
最大値：\( \ f\left( a+1\right)=a^2 \ \)
すなわち、 \( \ a \leq 1 \lt \frac{2a+1}{2} \ \)
整理して \( \ \frac{1}{2} \lt a \leq 1 \ \) のとき
最小値：\( \ f\left( 1\right)=0 \ \)
最大値：\( \ f\left( a+1\right)=a^2 \ \)
定義域の左端が軸よりも右にあるとき
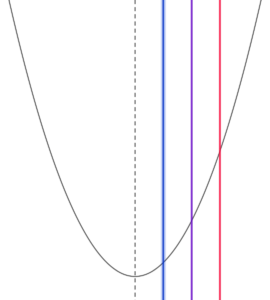
定義域の左端が放物線の軸よりも右側にある場合、
すなわち、 \( \ 1 \lt a \ \)のとき
最小値：\( \ f\left( a\right)=\left( a-1\right)^2 \ \)
最大値：\( \ f\left( a+1\right)=a^2 \ \)
すなわち、 \( \ 1 \lt a \ \)のとき
最小値：\( \ f\left( a\right)=\left( a-1\right)^2 \ \)
最大値：\( \ f\left( a+1\right)=a^2 \ \)
最小値
$$\begin{align}a^2&:\quad a \lt 0\quad のとき \\\\ 0&:\quad 0 \leq a \leq 1\quad のとき \\\\ \left( a-1\right)^2&:\quad 1 \lt a\quad のとき \end{align}$$最大値
$$\begin{align}\left( a-1\right)^2&:\quad a \lt \frac{1}{2} \quad のとき\\\\ \frac{1}{4}&:\quad a=\frac{1}{2}\quad のとき \\\\ a^2&:\quad \frac{1}{2} \lt a\quad のとき \end{align}$$こたえ
最小値$$\begin{align}a^2&:\quad a \lt 0\quad のとき \\\\ 0&:\quad 0 \leq a \leq 1\quad のとき \\\\ \left( a-1\right)^2&:\quad 1 \lt a\quad のとき \end{align}$$
最大値
$$\begin{align}\left( a-1\right)^2&:\quad a \lt \frac{1}{2} \quad のとき\\\\ \frac{1}{4}&:\quad a=\frac{1}{2}\quad のとき \\\\ a^2&:\quad \frac{1}{2} \lt a\quad のとき \end{align}$$ もう少し、複雑（？）な問題もあります。
よかったら、こちらもどうぞ。
https://makelemonadejp.com/yc-237共有:
プロフィール
Author Profile