高校数学の「3次関数の極値と実数解」に関する問題を解いてみる。（Yahoo!知恵袋より）
問題
(1) \( \ f\left( x\right) \ \)の極大値は \( \ \frac{\color{#0004fc}{ア}}{\color{#0004fc}{イウ}}a^3+\color{#0004fc}{エ}a \ \)であり, 極小値は\( \ \color{#0004fc}{オ}a^3+\color{#0004fc}{カ}a \ \) である。
$$\begin{align}f’\left( x\right)=&3x^2-2ax-a^2 \\ f’\left( x\right)=&0\quad となる \ x \ を求める. \\ \left( x-a\right)\left( 3x+a\right)=&0\\ x=&a\quad ,\quad x=-\frac{a}{3} \end{align}$$
増減表は以下の通り.
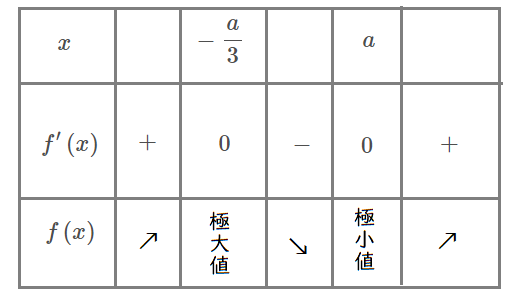
極大値は
$$f\left( -\frac{a}{3}\right)=\frac{\color{#0004fc}{5}}{\color{#0004fc}{27}}a^3+\color{#0004fc}{9}a$$
極小値は
$$f\left( a\right)=\color{#0004fc}{-}a^3+\color{#0004fc}{9}a$$
\( \ a \ \)が正の範囲で変化すると,\( \ g\left( a\right) \ \)は\( \ a=\sqrt{\color{#0004fc}{キ}} \ \)のとき,最大値\( \ \color{#0004fc}{ク}\sqrt{\color{#0004fc}{ケ}} \ \)をとる。
$$\begin{align}g\left( a\right)=&-a^3+9a \\ =&-a\left( a^2-9\right) \\ =&-a\left( a+3\right)\left( a-3\right) \quad より\end{align}$$
グラフは以下の通り.
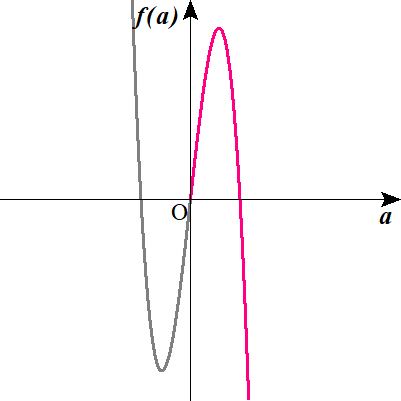
さらに,グラフより極大値が最大値になるといえるから,
$$\begin{align}g’\left( a\right)=&-3a^2+9=0 \\ a=& \pm \sqrt{3} \\ a \gt 0\quad より \ a=&\sqrt{3}\\ \\ a&=\sqrt{\color{#0004fc}{3}} \ のとき,\\ 最大値 \ &\color{#0004fc}{6}\sqrt{\color{#0004fc}{3}} \ をとる。 \end{align}$$
$$f\left( x\right)=0\quad が2つの異なる実数解を持つのは以下の2通り.$$
$$ⅰ）\quad 極小値が \ 0 \ のとき$$
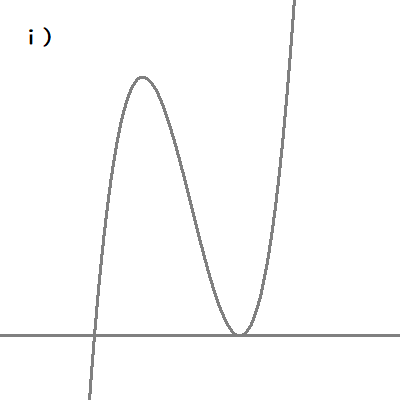
$$\begin{align}-a^3+9a=&0 \\ -a\left( a+3\right)\left( a-3\right)=&0 \\ a=&-3 \ , \ 0 \ , \ 3\\ ただし,\quad a \gt &0\quad より\\ a=&3 \end{align}$$
$$ⅱ）\quad 極大値が \ 0 \ のとき$$
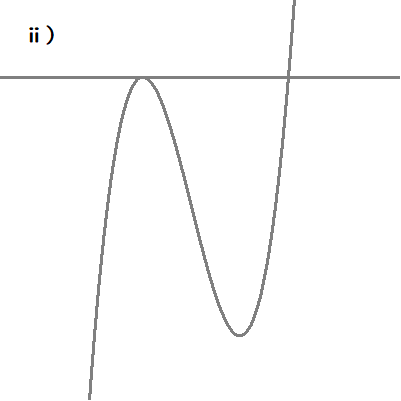
$$\begin{align}\frac{5}{27}a^3+9a=&0 \\ 実数解は\quad a=&0 \\ ただし,\quad a \gt &0\quad より\quad a=0\quad は不適. \end{align}$$
以上より
$$\begin{align}a=&\color{#0004fc}{3} \quad のとき,実数解の一つは, \ x=3\quad である.\\ &もう一つの実数解を \ x=-\alpha \ \left( \alpha \ ha
正の実数\right) \ とする. \\ f\left( x\right)=&\left( x-3\right)^2\left( x+\alpha\right)\\ f\left( x\right)=&0\quad を解いて,\\ \alpha=&3\\ \\ x=&\color{#0004fc}{3}\quad ,\quad \color{#0004fc}{-3} \end{align}$$
