高校数学の「図形の計量(入試過去問)」に関する問題を解いてみる。(Yahoo!知恵袋より)

[mathjax]
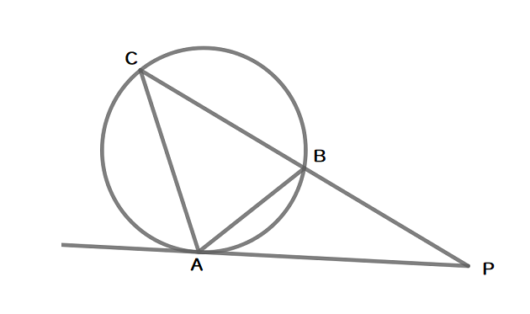
次に,\( \ \sin \angle \mathrm{BCA}=\frac{\sqrt{\color{#0004fc}{キ}}}{\color{#0004fc}{ク}} \ \)であり,\( \ \triangle \mathrm{ABC} \ \)の面積は\( \ \frac{\color{#0004fc}{ケ}\sqrt{\color{#0004fc}{コ}}}{\color{#0004fc}{サ}} \ \)である。
余弦定理より
$$\begin{align}\frac{3}{4}=&\frac{3^2+6^2-\mathrm{BP}^2}{2\cdot 3\cdot 6} \\\\ \mathrm{BP}^2=&18\\\\ \quad \mathrm{BP} \gt 0\quad より \\\\ \mathrm{BP}=&\color{#0004fc}{3}\sqrt{\color{#0004fc}{2}} \end{align}$$
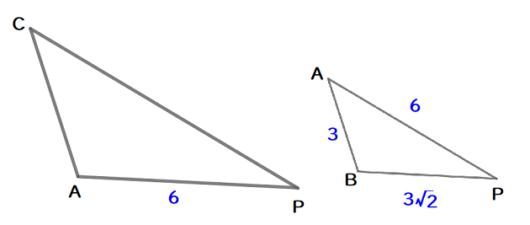
$$\begin{align}\mathrm{AP}:\mathrm{BP}=&\mathrm{CA}:\mathrm{AB} \\\\ 6:3\sqrt{2}=&\mathrm{CA}:3 \\\\ \mathrm{AC}=&\color{#0004fc}{3}\sqrt{\color{#0004fc}{2}} \end{align}$$
方べきの定理より
$$\begin{align}\mathrm{AP}^2=&\mathrm{CP}\cdot \mathrm{BP} \\\\ 6^2=&\left( \mathrm{BC}+\mathrm{BP}\right)\cdot \mathrm{BP} \\\\ \mathrm{BC}=&\color{#0004fc}{3}\sqrt{\color{#0004fc}{2}} \end{align}$$
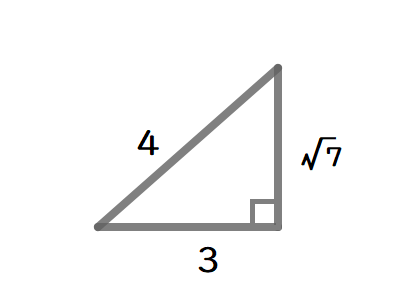
$$\begin{align}\sin \angle \mathrm{BCA}=&\sin \angle \mathrm{BAP} \\\\ \cos \angle \mathrm{BAP}=&\frac{3}{4}\quad より \\\\ \sin \angle \mathrm{BCA}=&\frac{\sqrt{\color{#0004fc}{7}}}{\color{#0004fc}{4}} \end{align}$$
$$\begin{align}面積を \ \mathrm{S}\quad &とする. \\\\ \mathrm{S}=&\frac{1}{2}\cdot \left( 3\sqrt{2}\right)^2\cdot \frac{\sqrt{7}}{4} \\\\ =&\frac{\color{#0004fc}{9}\sqrt{\color{#0004fc}{7}}}{\color{#0004fc}{4}} \end{align}$$
また,\( \ \triangle \mathrm{ABC} \ \)の重心を\( \ \mathrm{G} \ \)とすると,\( \ \mathrm{CG}=\sqrt{\color{#0004fc}{ソ}} \ \)である。
正弦定理より
$$\begin{align}\frac{\mathrm{AB}}{\sin \angle \mathrm{ACB}}=&2\mathrm{CO} \\\\ 3\times \frac{4}{\sqrt{7}}\times \frac{1}{2}=&\mathrm{CO} \\\\ \mathrm{CO}=&\frac{\color{#0004fc}{6}\sqrt{\color{#0004fc}{7}}}{\color{#0004fc}{7}} \end{align}$$
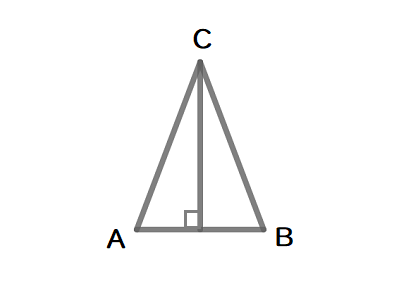
$$\begin{align}\triangle \mathrm{ABC}\quad は& \ \mathrm{AC}=\mathrm{BC}\quad の二等辺三角形. \\\\ 重心は&中線の交点であり, \\\\ &頂点\mathrm{C}\quad から辺\mathrm{AB}にひいた中線は,辺\mathrm{AB}\quad と垂直に交わる. \\\\ &頂点\mathrm{C}\quad から辺\mathrm{AB}\quad に引いた中線の交点を\mathrm{H}\quad とする. \end{align}$$
$$\begin{align}\triangle \mathrm{CHA}\quad &において,三平方の定理より \\\\ \mathrm{CH}=&\sqrt{18-\frac{9}{4}}=\frac{3\sqrt{7}}{2} \\\\ \ &重心は中線を \ 2:1 \ に内分するので,\\\\ \mathrm{CG}=&\frac{2}{3}\times \mathrm{CH}=\sqrt{\color{#0004fc}{7}} \end{align}$$
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません