高校数学の「放物線の平行移動と実数解の条件」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年12月27日2023年1月14日二次関数実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

放物線の平行移動は「頂点」で考える。

Lukia

放物線の式を見たら、平方完成して頂点や軸の位置を把握してしまいましょう。
曲線で平行移動させると、頭が混乱してしまいます。

(1)
$$\begin{align}条件より,平行移動後の頂点は\quad &\left( a \ , \ -a-2\right)\quad と表せる. \\\\ また、平行移動後の放物線は\quad y=&\left( x-a\right)^2-a-2\quad で表される.\\\\ a=1のとき,頂点は \ &\left( 1 \ , \ -3\right)\quad であるから,\\\\ y=\left( x-1\right)^2-3=& x^2-2x-2\end{align}$$

(2)
$$\begin{align}平行移動した放物線 \ y=&\left( x-a\right)^2-a-2\quad が原点を通るから, \\\\ &a^2-a-2=0 \\\\ これを解いて\quad \quad &a=2 \ , \ a=-1\end{align}$$
$$\begin{align}a=&2\quad のとき\\\\ \quad \quad y=\left( x-2\right)^2-4=x^2-4x \\\\ a=&-1\quad のとき\\\\ \quad \quad y=\left( x+1\right)^2-1=x^2+2x \end{align}$$
(3)
$$\begin{align}f\left( x\right)=&\left( x-a\right)^2-a-2\quad とする. \\\\放物線と&x軸とが異なる2点で交わるから, \\\\ -a-2 \lt &0\quad \cdots \ ①\\\\ 2交点の&x座標がともに1より大きくなるためには,\\\\ 1 \lt &a\quad \left(軸の位置\right) かつ\quad f\left( 1\right) \gt 0\quad である必要がある. \quad \cdots \ ② \end{align}$$

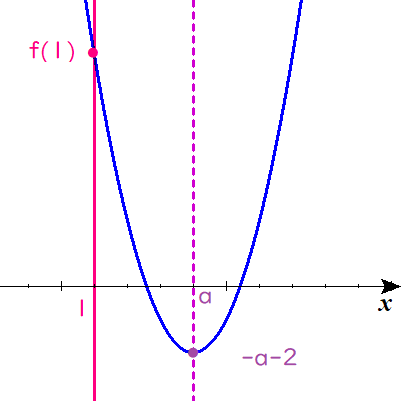
$$\begin{align}-2 \lt &a\quad \cdots \ ① \\\\ \left( 1-a\right)^2-a-2 \gt &0\\\\ a^2-3a-1 \gt &0\\\\ &a \lt \frac{3-\sqrt{13}}{2} \ , \ \frac{3+\sqrt{13}}{2} \lt a \\\\ ただし \ &1 \lt a \ であるから, \\\\ \frac{3+\sqrt{13}}{2} \lt a\quad \cdots \ ②\end{align}$$
$$① \ , \ ② \ より\quad \quad \frac{3+\sqrt{13}}{2} \lt a$$

こたえ

$$\begin{align}\left( 1\right)\quad \quad y=&x^2-2x-2 \\\\ \left( 2\right)\quad \quad y=&x^2-4x \\\\または \ y=&x^2+2x\\\\ \left( 3\right)\quad \quad & \frac{3+\sqrt{13}}{2} \lt a \end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。