高校数学の「放物線の軸の存在範囲」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年11月29日2023年1月14日二次関数実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

まずは平方完成。

$$\begin{align}y=&x^2+2ax+9 \\\\ =&\left( x+a\right)^2-a^2+9\quad より, \\\\この放物線は&頂点が\left( -a \ , \ -a^2+9\right) \ にある下に凸の関数である. \end{align}$$

4つの象限

Lukia

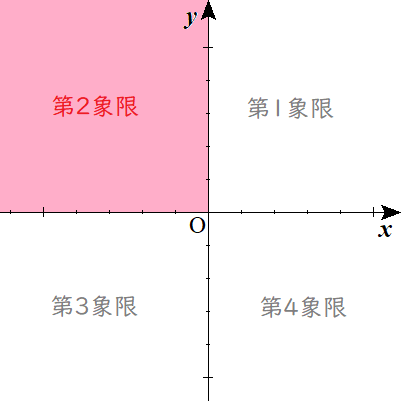
ここで、\(xy\)平面上に存在する4つの象限を確認しておきましょう。

Lukia

上の図のように、\(x\)軸と\(y\)軸によって平面が4つに分けられます。
そして、右上を「第1象限」とし、以降は、（右上から）反時計回りに第2象限、第3象限、第4象限となります。
図より、「第2象限は\(x \lt 0 \ かつ \ y \gt 0\quad \)（\(x\)は負 かつ \(y\)は正）」
だとわかりますね。

象限と頂点の条件より定数aの範囲を求める。

$$\begin{align}頂点\left( -a \ , \ -a^2+9\right) \ は&第2象限にあるので \\\\ -a \lt &0\quad すなわち \\\\ \color{red}{a \gt 0}\cdots① \\\\ -a^2+9 \gt &0\\\\ a^2-9 \lt &0\\\\ \left( a-3\right)\left( a+3\right) \lt &0 \quad \\\\すなわち\quad   \color{#0004fc}{-3 \lt a \lt 3}\cdots② \end{align}$$

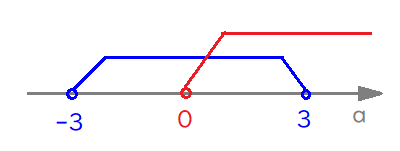
$$求める定数aの値の範囲は\quad 0 \lt a \lt 3$$

こたえ

$$0 \lt a \lt 3$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。