高校数学の「2つも絶対値がある不等式」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年12月11日2023年1月14日数と式実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

「絶対値」と思うから難しいんです。

事件は、スイーツのお店で起こりました。
なぜか、パラレルワールドにも「Yahoo!知恵袋」はあり、恐竜とはいえ今時の高校生、ディノさんもちょいちょいチェックしているようです。
早々にスイーツをたいらげ、スマホをいじっていたディノさんでしたが・・・。

ディノ

なんじゃこりゃ～！

Lukia

？と言いますと？（松田優作を知ってるのか？）

ディノ

絶対値が絶対値にはさまれてるぞ！

Lukia

そうですねぇ。なんとかしなきゃですねぇ。

ディノ

パンケーキ食ってる場合かよ。ど～すりゃいいんだ～～！！
（ディノさんの雄叫びで店が軽く震える）

Lukia

ディノさん、落ち着いてッ。
（あ～あ、お店の警報が鳴っちゃったよ・・・）
今のディノさんなら、必ず解けますから。

私は、周囲のおびえた目をしたお客さんたちに謝り、警報を止めるのにあわてふためく店員さんに謝りました。

Lukia

（なんで、私がディノさんの代わりに謝ってんだか・・・）
「絶対値」は、「絶対値」と思うから難しいんですよ。

ディノ

なんだそりゃ。禅問答か。

Lukia

いえいえ。「絶対値」の記号を別のものに見立てれば、
解法はおのずとわかるはずです。

ディノ

なんだ、その「別のもの」って。

Lukia

じゃ、やってみますか。

ディノ

よし！じゃ、早くパンケーキ食っちまえ！
なんなら、オレが手伝ってやるぞ。

Lukia

だめっ！このパンケーキは私のですッ！

むくれるディノさんを尻目に、残っていたパンケーキを惜しむように食べました。

優先順位を決める。

Lukia

さて、ディノさん、
もしもこの式が、\(\left( \left( x-1\right)-1\right) \lt 1\)　だったら、どうします？

ディノ

そりゃ、内側のカッコをはずしてだな・・・

$$\begin{align}\left( \left( x-1\right)-1\right)& \lt 1 \\\\ \left( x-1-1\right)& \lt 1 \\\\ x-2& \lt 1\\\\ x& \lt 3 \end{align}$$

ディノ

こういう風に解くな。

Lukia

カッコは、おそらく小学校の算数ぐらいから見ていると思いますが、
これは、簡単に言うと、数学や算数における「優先順位」を示すものですよね。
カッコの中を先に計算して、カッコをはずしていくはずです。
今回のように、カッコの入れ子構造になっている場合、より内側のカッコから外していく必要がありますよね。

ディノ

ということは、絶対値も内側から外せばいいのか。

Lukia

そのとおりです。
ひとまず、\(y=\vert \vert x-1 \vert -1 \vert\) としてグラフなり、式なりを考えてみましょう。

1）
$$\begin{align}1 \leq &x\quad のとき \\\\ y=&\vert x-1-1 \vert=\vert x-2 \vert \end{align}$$
2)
$$\begin{align}x \lt &1\quad のとき \\\\ y=&\vert -x+1-1 \vert=\vert -x \vert \end{align}$$

ディノ

ひとまず、ひとつの絶対値記号がはずれたな。

Lukia

はい。でも、まだもうひとつが残っていますね。
1）や2）の\(x\)の範囲はおおもとなので、無視しないようにして、さらに絶対値記号をはずしていきましょう。

内側から絶対値記号はずしてグラフを描く。

1)
$$\begin{align}1 \leq &x \lt 2\quad のとき \\\\ y=&-x+2 \cdotsⅰ\\\\ 2 \leq &x\quad のとき\\\\ y=&x-2\cdotsⅱ \end{align}$$

2）
$$\begin{align}0 \lt &x \lt 1\quad のとき \\\\ y=&x\cdotsⅲ \\\\ x \leq &0\quad のとき\\\\ y=&-x\cdotsⅳ\end{align}$$

Lukia

ⅰからⅳまでをグラフにまとめると、以下の図の青い線のようになりますね。

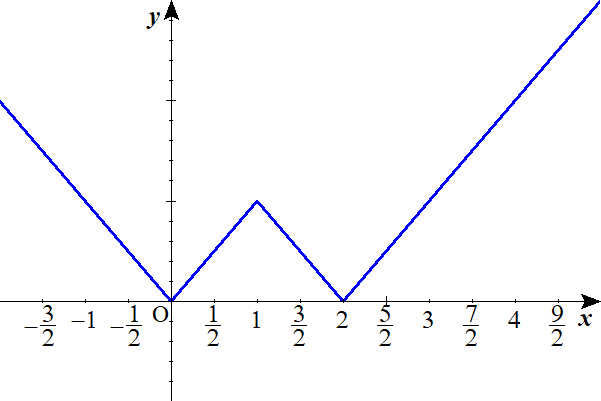
不等式を解く。

Lukia

グラフが描けたのですから、このグラフに\(y=1\)を描き加えて、条件を満たす整数\(x\)をさがしてみましょう。

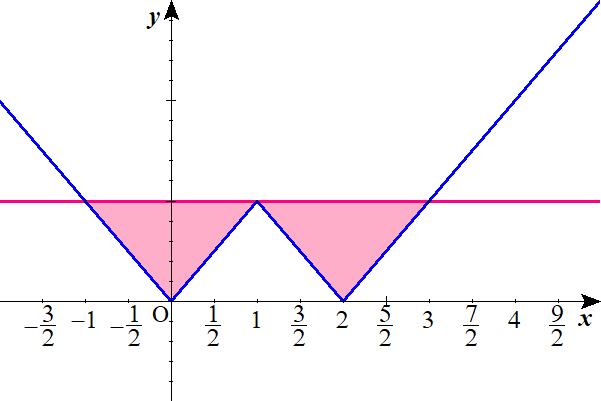
Lukia

上の図のピンクで塗りつぶされた下向き三角形の部分が条件を満たす領域です。

ディノ

ピンクの直線と、ブルーの直線の交点部分は含まないんだよな。
ということは、\(-1 \lt x \lt 1\)と\(1 \lt x \lt 3\)ということになる。

Lukia

そうですね。では、二つの範囲に含まれている整数はいくつですか。

ディノ

\(0\)と\(2\)だ。

Lukia

ということは、題意を満たす整数\(x\)の個数は・・・

ディノ

2個だな♪

こたえ

2個

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。