高校数学の「図形と計量」に関する問題を解いてみる。(Yahoo!知恵袋より)

[mathjax]
\( \ \triangle \mathrm{ABC} \ \)の面積は\( \ \frac{21\sqrt{15}}{4} \ \)である。
また,点\( \ \mathrm{C} \ \)をとおり,辺\( \ \mathrm{AB} \ \)と平行な直線と,\( \ \angle \mathrm{ABC} \ \)の二等分線が交わる点を\( \ \mathrm{D} \ \)とするとき,
線分\( \ \mathrm{AD} \ \)の長さはいくらか。
「逆算力」を持とう。

Lukia
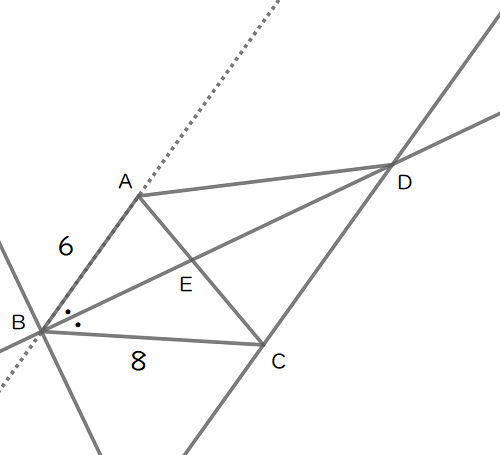
こんな図を限られた時間で、なるべく正確にかくのは難しそうですね。

Lukia
いろいろなアプローチがあると思いますが、こういう幾何の問題は、特に「逆算する力」が求められるように思います。
もっというと、辺\( \ \mathrm{AD} \ \)を求めるのに、どの三角形の情報がわかればよいのか。ということをあらかじめ見極めておく力ともいえると思います。

Lukia
目的地(情報を得たい三角形)が定まらぬまま、なんとなくやっていると、そのうちどんどんドツボにはまっていってしまいます。

Lukia
目的地が定まったら解いていくだけ。


Lukia
辺\( \ \mathrm{AD} \ \)を求めるには、\( \ \triangle \mathrm{ACD} \ \)の情報が得られればよさそうですね。

Lukia
$$\begin{align}\triangle \mathrm{ABC}について&余弦定理より \\\\ \cos \angle \mathrm{BAC}=&\frac{\mathrm{AB}^2+\mathrm{AC}^2-\mathrm{BC}^2}{2\mathrm{AB}\cdot \mathrm{AC}}=\frac{1}{4} \\\\ また,平行線の錯角より&\angle \mathrm{BAC}=\angle \mathrm{ACD}\quad であるから,\\\\ \cos \angle \mathrm{ACD}=&\frac{1}{4}\quad \cdots\cdots\quad ① \end{align}$$
$$\begin{align}線分\mathrm{BE}は,&\angle \mathrm{ABC}の二等分線だから, \\\\ \mathrm{AB}:\mathrm{CB}=&\mathrm{AE}:\mathrm{EC}=3:4 \\\\ &\left( 点\mathrm{E} \ は辺 \ \mathrm{AB} \ を3:4に内分するといえる\right) \end{align}$$

Lukia
$$\begin{align}\triangle \mathrm{EAB}\quad と& \ \triangle \mathrm{ECD}\quad において, \\\\ \angle \mathrm{AEB}=&\angle \mathrm{CED}\quad \left( 対頂角\right) \\\\ \angle \mathrm{ABE}=&\angle \mathrm{CDE}\quad \left( 平行線の錯角\right)\quad より\\\\ \triangle \mathrm{EAB}\sim &\triangle \mathrm{ECD}\quad であり,\\\\ 相似比は,&3:4\quad である.\\\\ ゆえに,\quad \mathrm{CD}=&8\quad \cdots\cdots\quad ② \end{align}$$
$$\begin{align}\triangle \mathrm{ACD}\quad において,&余弦定理より, \\\\ \cos \angle \mathrm{ACD}=&\frac{\mathrm{AC}^2+\mathrm{CD}^2-\mathrm{AD}^2}{2\mathrm{AC}\cdot \mathrm{CD}} \\\\ \frac{1}{4}=&\frac{49+64-\mathrm{AD}^2}{2\cdot 7\cdot 8}\\\\ \mathrm{AD}^2=&85\\\\ \mathrm{AD}=&\sqrt{85}\quad \left( \mathrm{AD} \gt 0\quad より\right) \end{align}$$
こたえ
$$\mathrm{AD}=\sqrt{85}$$










ディスカッション
コメント一覧
まだ、コメントがありません