高校数学の「内接円の半径」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年10月20日2023年1月15日図形の性質実用数学技能検定（数学検定 数検),数検2級,数検準2級

[mathjax]

解法

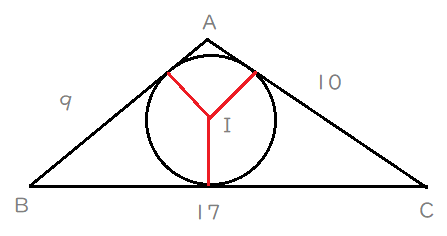
Lukia

グラフは、GRAPESで描けるようになったのですが、
三角形などの図形はまだうまく描けません。
数値が正確ではないのですが、おおよその図でイメージしてください。

$$\begin{align}\triangle \mathrm{\mathrm{ABC}}&の面積を\mathrm{S}とする。 \\\\ \mathrm{S}=&\frac{1}{2}\mathrm{AB}\cdot \mathrm{BC}\cdot \sin \angle \mathrm{\mathrm{B}} \\\\ =&\frac{1}{2}\cdot 9\cdot 17\cdot \frac{8}{17}\\\\=&36 \end{align}$$
$$\begin{align}また、\triangle \mathrm{\mathrm{ABC}}&の内接円の中心を\mathrm{I}とすると、 \\\\ \mathrm{S}=&\triangle \mathrm{\mathrm{IBC}}+\triangle \mathrm{\mathrm{ICA}}+\triangle \mathrm{\mathrm{IAB}} \\\\ =&\frac{1}{2}r\left( \mathrm{AB+BC+CA}\right) より\end{align}$$
$$\begin{align}36=&\frac{1}{2}r\left( 9+17+10\right) \\\\ 36=&\frac{1}{2}r\cdot 36 \\\\ r=&2 \end{align}$$

こたえ

$$r=2$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。