高校数学の「二次関数の頂点」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年11月30日2023年1月14日二次関数実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

解法

$$\begin{align}求める放物線の方程式を\quad y=a\left( x-1\right)^2+9\cdots★\quad とおく. \\\\頂点のy座標が \ 9 \gt 0 \ であるので, \\\\求める放物線は\color{#0004fc}{上に凸} \ である.\\\\ ゆえに \ a \lt 0 \ である. \end{align}$$

Lukia

頂点が\(x\)軸のはるか上にありますからね。
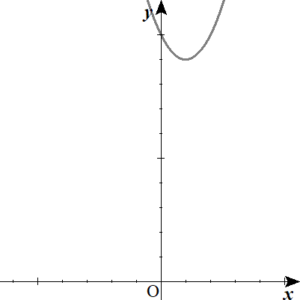
下の図のような、下に凸の放物線はありえませんよね。

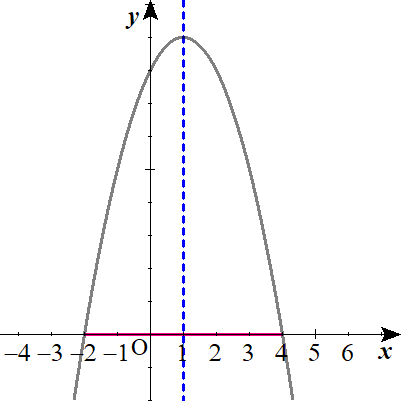
$$\begin{align}&また, \ 放物線がx軸から切り取る長さが6 \ ということから,\\\\&放物線は \ \left( -2 \ , \ 0\right) \ , \ \left( 4 \ , \ 0\right) \ を通るとわかる. \\\\ &★に \ \left( -2 \ , \ 0\right) \ を代入して,\\\\ &0=a\left( -2-1\right)^2+9\\\\ &9a=-9\\\\ &a=-1\end{align}$$
$$\begin{align}ゆえに,&求める放物線の方程式は \\\\ y=&-\left( x-1\right)^2+9 \\\\ y=&-x^2+2x+8 \end{align}$$

こたえ

$$y=-x^2+2x+8$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。