高校数学の「空間ベクトルの内分とその比」に関する問題を解いてみる。（Yahoo!知恵袋より）
[mathjax]
直線\(\mathrm{OG}\)と平面\(\mathrm{DBE}\)の交点を\(\mathrm{P}\)とするとき、\(\mathrm{OP:OG}\)を求めよ。
不正確でもいいから図を描こう。
Lukia
解き始めから正確な図が描けることはほとんどありません。
でも、「描かないよりは絶対マシ。」です。
大学入試センター試験では、はじめはうす～く描いておいて、ある程度辺の長さや角度がわかってきたところで、改めてできるだけ正確な図に描き直しましょう。
（図が正確になるとわかることなどもあるので、テキトーな図のままでは完答できない。なんて問題もあります）
Lukia
「図形の頂点の記号は、反時計回りに描くと解きやすい」です。
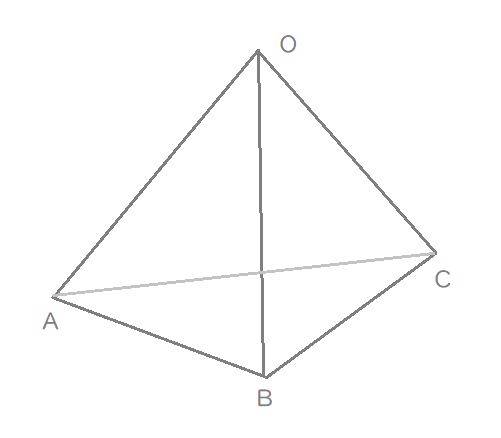
Lukia
辺の内分比や重心の位置を書き込みます。
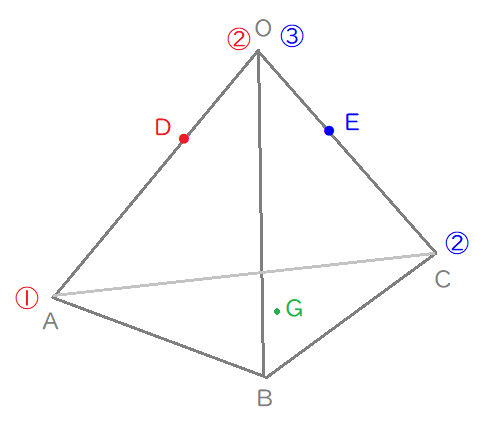
Lukia
辺\(\mathrm{OA}\)のほうは、3倍し、辺\(\mathrm{OC}\)のほうは2倍すれば、統一できそうですね。
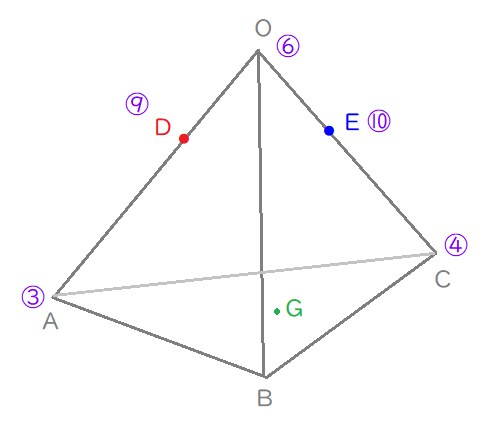
わかっていることを書き出しながら解いていく。
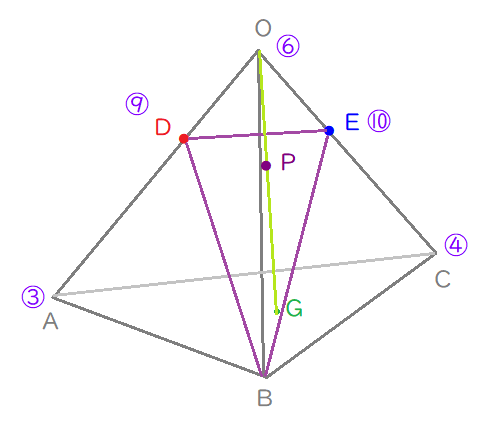
$$\begin{align}\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{a}} \ , \ \overrightarrow{\mathrm{OB}}=&\overrightarrow{\mathrm{b}} \ , \ \overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{c}}\quad とする。\\\\条件より \ \overrightarrow{\mathrm{OG}}=&\frac{1}{3}\left( \overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{c}}\right) \\\\\overrightarrow{\mathrm{OP}}=&k\overrightarrow{\mathrm{OG}}\quad \left( kは \ k \gt 0 \ を満たす実数\right) \ とする. \end{align}$$
$$\begin{align}また,点\mathrm{P}は \ 平面&\mathrm{DEB}上に存在するから, \\\\ \overrightarrow{\mathrm{OP}}=&l\overrightarrow{\mathrm{OD}}+m\overrightarrow{\mathrm{OB}}+n\overrightarrow{\mathrm{OE}} \ \left( l+m+n=1 \ を満たす\right) \ と表せる。\\\\ \overrightarrow{\mathrm{OP}}=&l\cdot \frac{3}{9}\overrightarrow{\mathrm{a}}+m\overrightarrow{\mathrm{b}}+\frac{2}{5}n\overrightarrow{\mathrm{c}} \end{align}$$
以上より,
$$\begin{align}\frac{k}{3}=\frac{1}{3}l\quad すなわち \ l=&k \\\\\frac{k}{3}=m\quad すなわち \ m=&\frac{k}{3}\\\\\frac{k}{3}=\frac{2}{5}n\quad すなわち \ n=\frac{k}{3}\times \frac{5}{2}=&\frac{5}{6}k \end{align}$$
ここで,
$$\begin{align}l+m+n=&k+\frac{k}{3}+\frac{5}{6}k \\\\ =&\frac{k}{6}\left(6+2+5 \right) \\\\ \frac{13}{6}k=&1\quad より\\\\ \\\\ k=&\frac{6}{13} \end{align}$$
$$ゆえに\quad \mathrm{OP:OG}=6:13$$
Lukia
ま、練習がてら。ということで・・・
こたえ
$$\mathrm{OP:OG}=6:13$$
共有:
プロフィール
