高校数学の「二次方程式が実数解をもつ条件(見た目は三角関数)」に関する問題を解いてみる。(Yahoo!知恵袋より)

読了時間: 約3分26秒
[mathjax]
問題
\(0 \leq \theta \leq 2\pi \ \)のとき,
方程式\( \ \cos^{2} \theta-4\cos \theta+k=0 \ \)が解をもつような定数\(k\)の値の範囲を求めよ。
方程式\( \ \cos^{2} \theta-4\cos \theta+k=0 \ \)が解をもつような定数\(k\)の値の範囲を求めよ。
xに置換して定義域を変換する。
$$\begin{align}\cos \theta=&x \ とする.\\\\ x^2-4x+k=&0\quad \left( -1 \leq x \leq 1\right) \\\\ ここで \ f\left( x\right)=&x^2-4x+k\\\\ =&\left( x-2\right)^2+k-4 \quad \left( -1 \leq x \leq 1\right) \quad とする.\end{align}$$
軸と定義域の関係から放物線を想定する。

Lukia
定義域\( \ -1 \leq x \leq 1 \ \)が明らかに軸(\(x=2\))より左側にあるので、放物線のグラフは以下の図しか想定できません。
(数値と幅は対応させていませんので、あしからず。)

(数値と幅は対応させていませんので、あしからず。)
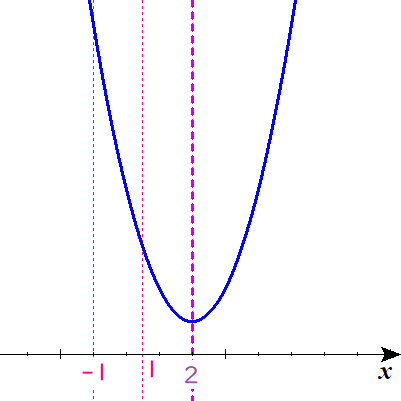
放物線f(x)を上下に動かしてみる。

Lukia
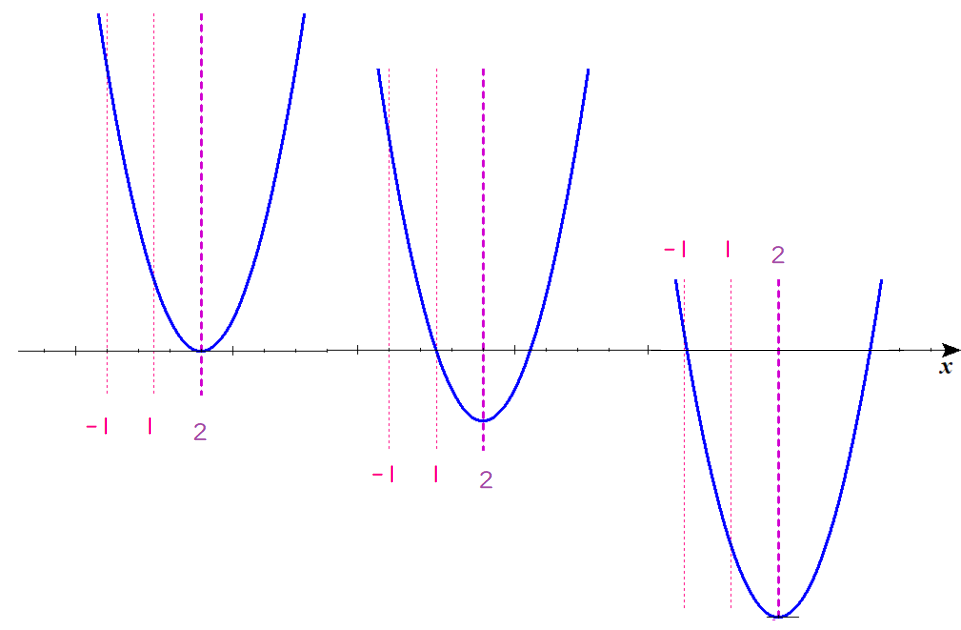
いよいよ、\(f\left( x\right)\)が実数解をもつような定数\(k\)の値の範囲を求めていきます。ここからは、放物線の頂点を移動させながら、定義域の端点のふるまいを見ていきます。
以下の図を参照しながら説明します。
以下の図を参照しながら説明します。

Lukia
\(f\left( x\right)\)は、下に凸の放物線です。
ということは、少なくとも1つの実数解をもつためには、頂点の\(y\)座標、すなわち\(k-4\)が、\(x\)軸に接するか、それよりも下にあることが必要となります。
軸\( \ x=2 \ \)に注目したまま、図を左から右に見てください。
放物線そのものは、(定義域は無視)確実に\(x\)軸と交わって(実数解をもって)いますね。
ということは、少なくとも1つの実数解をもつためには、頂点の\(y\)座標、すなわち\(k-4\)が、\(x\)軸に接するか、それよりも下にあることが必要となります。
軸\( \ x=2 \ \)に注目したまま、図を左から右に見てください。
放物線そのものは、(定義域は無視)確実に\(x\)軸と交わって(実数解をもって)いますね。

Lukia
次に、定義域の端点に着目します。


Lukia
図の左側の放物線は、軸が\(x\)軸と接していますが、
端点\( \ f\left( -1\right) \ \)または\( \ f\left( 1\right) \ \)は、\(x\)軸と交わってはいません。
つまりこの状態では、放物線そのものが実数解をもつ。という最低条件を満たしただけで、定義域内では条件を満たしていないことになります。
端点\( \ f\left( -1\right) \ \)または\( \ f\left( 1\right) \ \)は、\(x\)軸と交わってはいません。
つまりこの状態では、放物線そのものが実数解をもつ。という最低条件を満たしただけで、定義域内では条件を満たしていないことになります。

Lukia
図の真ん中の放物線は、頂点が\(x\)軸よりも下に移動していますね。
これにより、放物線自体は、実数解を2つもつ状態になっています。
定義域の右の端点\( \ f\left( 1\right) \ \)が\(x\)軸と交わったところから、いよいよ定義域に実数解が存在するようになります。
これにより、放物線自体は、実数解を2つもつ状態になっています。
定義域の右の端点\( \ f\left( 1\right) \ \)が\(x\)軸と交わったところから、いよいよ定義域に実数解が存在するようになります。


Lukia
図の右側の放物線は、頂点が\(x\)軸のかなり下に位置したことにより、
定義域の左の端点\( \ f\left( -1\right) \ \)が\(x\)軸と交わりました。
つまり、頂点の位置をぐいぐい下げていくことによって、定義域の左の端点も\(x\)軸に近づけられるということがわかりますね。
しかし、これがもう限界です。
これ以上頂点を下げると、左の端点すら、\(x\)軸よりも下に位置してしまいます。
定義域の左の端点\( \ f\left( -1\right) \ \)が\(x\)軸と交わりました。
つまり、頂点の位置をぐいぐい下げていくことによって、定義域の左の端点も\(x\)軸に近づけられるということがわかりますね。
しかし、これがもう限界です。
これ以上頂点を下げると、左の端点すら、\(x\)軸よりも下に位置してしまいます。
極端な状態を参考に条件を求める。

Lukia
「どこまでがギリか。」というのを試すのは、世の中にもいろいろありますね。
お給料や結婚相手の条件だったり、遅刻にならないためには、家を何時に出ればいいか。とか。
小さい子供がわがままを言って、親の許容範囲を探るなんてのもあります。(まぁ、親を試すのは年齢を問いませんかね。)
法律やルールなどもある意味、「ギリ」を設定しているものといえます。
お給料や結婚相手の条件だったり、遅刻にならないためには、家を何時に出ればいいか。とか。
小さい子供がわがままを言って、親の許容範囲を探るなんてのもあります。(まぁ、親を試すのは年齢を問いませんかね。)
法律やルールなどもある意味、「ギリ」を設定しているものといえます。
人間が「ギリ」を探るのは、
どこまでがセーフで、どこからがアウトか。というのを理解しておけば、セーフの範囲内で安全で自由にふるまえるからなんですね。

Lukia
数学でも同じことが言えると思います。
3つの放物線を用いて、実数解をもつ条件を探ってきましたが、
実は、真ん中の放物線は、補助的なものです。
定義域の右の端点は、定義域の左の端点と頂点が存在する軸に挟まれているので、言ってみれば、「ギリ」というよりは「思いっきりセーフ」にあたるんですね。
3つの放物線を用いて、実数解をもつ条件を探ってきましたが、
実は、真ん中の放物線は、補助的なものです。
定義域の右の端点は、定義域の左の端点と頂点が存在する軸に挟まれているので、言ってみれば、「ギリ」というよりは「思いっきりセーフ」にあたるんですね。

Lukia
長くなりましたが、問題の実数解をもつ条件を探るには、
図の左側と、右側の状態を、それぞれ数学語で表現することになります。
図の左側と、右側の状態を、それぞれ数学語で表現することになります。
$$\begin{align}f\left( x\right)=&\left( x-2\right)^2+k-4\quad が\\\\定義域\left( -1 \leq x \leq 1\right) \ &において実数解をもつためには\\\\ f\left( 2\right) \leq &0\quad かつ\quad f\left( -1\right) \geq 0\quad である必要がある. \\\\ &k-4 \leq 0\quad かつ\quad k+5 \geq 0\\\\ &-5 \leq k \leq 4 \end{align}$$
こたえ
$$-5 \leq k \leq 4$$
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません