Yahoo!知恵袋の高校数学カテゴリにあった「三角比と図形」に関する問題を解いてみる。（ちょっと難しい？）
[mathjax]
\(\sin \angle\mathrm{A}=\frac{4}{5} , \angle\mathrm{B}=30^{\circ} , a=16\) のとき、
辺\(b , c\) の長さを求めよ。
解法
Lukia
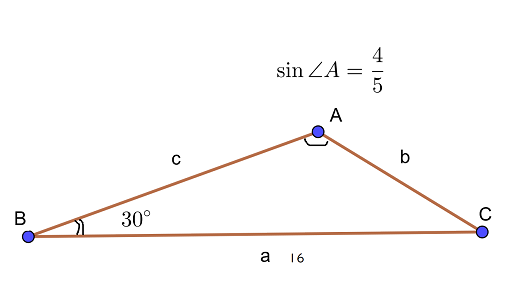
正弦定理を用いて。
Lukia
$$\begin{align}正弦定理より& \\\\ \frac{\sin \angle\mathrm{B}}{\sin \angle\mathrm{A}}=&\frac{b}{a} \\\\ b=&\frac{\sin \angle\mathrm{B}}{\sin \angle\mathrm{A}}\cdot a\\\\ =&\frac{1}{2}\times \frac{5}{4}\times 16\\\\ =&10 \end{align}$$
$$\Large ゆえに b=10$$
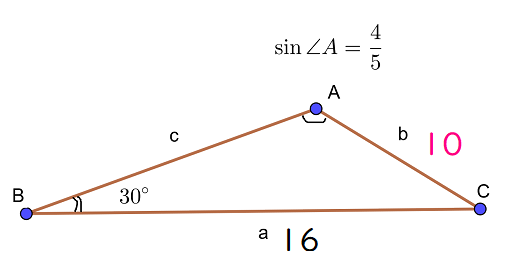
余弦定理を用いて。
Lukia
辺\(c\) の長さを求めてみます。
$$\Large \color{red}{\cos \angle\mathrm{B}=\frac{c^2+a^2-b^2}{2ca}} より、$$
$$\begin{align}\cos \angle\mathrm{B}=&\frac{c^2+16^2-10^2}{2c\cdot 16} \\\\ \frac{\sqrt{3}}{2}\times 2\cdot 16c=&c^2+4\cdot 4^3-4\cdot 25 \\\\ 16\sqrt{3}c=&c^2+4\times 39 \end{align}$$
$$\begin{align}c^2-16\sqrt{3}c=&-4\times 39 \\\\ \left( c-8\sqrt{3}\right)^2-64\times 3=&-4\times 39 \\\\ \left( c-8\sqrt{3}\right)^2=&12\left( 16-13\right)=36\\\\ c-8\sqrt{3}=& \pm 6\\\\ c=&8\sqrt{3} \pm 6 \end{align}$$
辺cの大きさはどちらも正しいの？
Lukia
\(\angle\mathrm{A}\)は、鋭角なのか鈍角なのかは書かれていません。
つまり、それぞれ場合分けをして本当に三角形として成立するかを確かめる必要があるので、ちょっと難しいのです。
辺cの大きさをはっきりイメージしてみる。
$$\begin{align}8\sqrt{3}=&\sqrt{192} より、\\\\ 13 \lt &8\sqrt{3} \lt 14 \\\\ ⅰ） 13+6 \lt &8\sqrt{3}+6 \lt 14+6\\\\ すなわち、19 \lt &8\sqrt{3}+6 \lt 20 \\\\ ⅱ）13-6 \lt &8\sqrt{3}-6 \lt 14-6\\\\ すなわち、7 \lt &8\sqrt{3}-6 \lt 8 \end{align}$$
Lukia
ちなみに、数直線上に三つの辺を表してみると、以下のようになります。
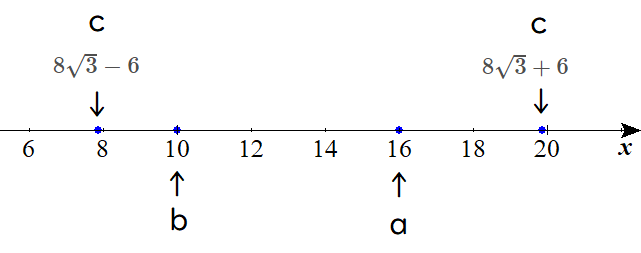
Lukia
辺\(c\)が最大辺になる場合がありますね。
∠Aが最大角の場合
$$\begin{align}\angle\mathrm{A}が最大角のとき、& 辺a が最大辺となる。\\\\ c \lt a かつ、a \lt b+c&が成り立つ必要がある。 \\\\ \ a-b \lt &c \lt a\\\\ すなわち、6 \lt &c \lt 16 を満たすcは、 \\\\ & \ c=8\sqrt{3}-6 \end{align}$$
∠Cが最大角の場合
$$\begin{align}\angle\mathrm{C}が最大角のとき、& 辺c が最大辺となる。\\\\ c \gt a かつ、c \lt a+b&が成り立つ必要がある。 \\\\ \ a \lt &c \lt a+b\\\\ すなわち、16 \lt &c \lt 26 を満たすcは、 \\\\ & \ c=8\sqrt{3}+6 \end{align}$$
Lukia
調べなくてもいいじゃん。と思いがちですが、
問題によっては、どちらかが不適になる場合もあります。
出題者は、こういうところまで気持ちが行き届いている人物なのかどうかを試しています。
入試の場合は、よいピーアールになりますので、きちんと場合分けをして調べましょう。
こたえ
$$\Large b=10$$
$$\Large c=8\sqrt{3} \pm 6$$
共有:
プロフィール
