高校数学の「ベクトル（内積・三角形の面積公式）」に関する問題を解いてみる。（Yahoo!知恵袋より）
[mathjax]
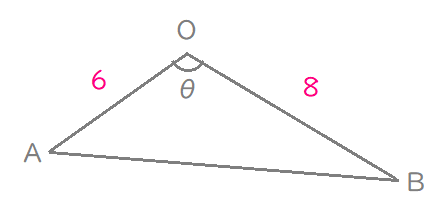
三角比を使った面積公式からサインを求める
Lukia
ここは、ベクトルの範囲というわけではないです。
$$\begin{align}\angle \mathrm{AOB}=&\theta \ とする。\\\\ \mathrm{S}=&\frac{1}{2}\mathrm{OA}\cdot \mathrm{OB}\sin \theta \ より\\\\ 9\sqrt{7}=&\frac{1}{2}\cdot 6\cdot 8\cdot \sin \theta\\\\ \sin \theta=&\frac{3\sqrt{7}}{8} \end{align}$$
（その1）三角比を用いて内積を求める。
Lukia
三平方の定理を用いて、\(\cos \theta\)の値が求められればいいだけなので、
以下の直角三角形を使います。
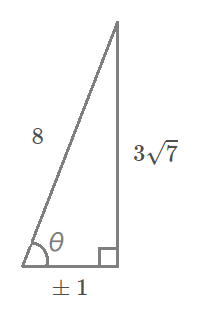
$$\begin{align}\cos \theta=&\frac{ \pm 1}{8} \\\\ ただし \ \theta \ は鈍角なので、 \\\\ \cos \theta=&-\frac{1}{8} \end{align}$$
$$\begin{align}\cos \theta=&\frac{\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}}{\vert \overrightarrow{\mathrm{OA}} \vert\vert \overrightarrow{\mathrm{OB}} \vert} \\\\ \\\\ -\frac{1}{8}=&\frac{\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}}{6\cdot 8} \\\\ \\\\ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=&-6 \end{align}$$
（その2）ベクトルの三角形の面積公式を用いて内積を求める。
https://makelemonadejp.com/area-of-a-triangle/平面ベクトルの三角形の面積公式は、
$$\Large \mathrm{S}=\frac{1}{2}\sqrt{\vert \overrightarrow{\mathrm{OA}} \vert^2\vert \overrightarrow{\mathrm{OB}} \vert^2-\left( \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}\right)^2}$$
で求められます。
$$\begin{align}9\sqrt{7}=&\frac{1}{2}\sqrt{6^2\cdot 8^2-\left( \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}\right)^2} \\\\ 両辺を2乗して \\\\ 81\cdot 7=&\frac{1}{4}\left( 6^2\cdot 8^2-\left( \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}\right)^2\right)\\\\ 36\left( 63-64\right)=&-\left( \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}\right)^2\\\\ \\\\ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=& \pm 6\end{align}$$
$$\begin{align}ここで、 \ &\theta \ は鈍角であるから、 \\\\ \cos \theta \lt &0\\\\ \\\\ゆえに \ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=&-6 \end{align}$$
どちらでも解けますが・・・
Lukia
さて、どちらで解くべきか。ということについて自分なりに場合分けをしてみました。
Lukia
\(\cos \theta\)を求めよ。となってないので、わざわざ求めるのももったいない気もしますが、
計算量が少ないので、時短にはなりますね。
Lukia
（その2）のような煩雑な計算をするわけにはいきません。
ですから、単元は「平面ベクトル」なのですが、三角比を使えるならおおいに利用して確実に解き進めましょう。
Lukia
平方根をはずすのが苦手な人は、こういう問題になるべく当たって、練習しておきましょうね。
こたえ
$$\Large \begin{align}\sin \angle \mathrm{AOB}=&\frac{3\sqrt{7}}{8} \\\\ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=&-6\end{align}$$
共有:
プロフィール
