高校数学の「正弦定理から三角形の形状を考える」問題を解いてみる。(Yahoo!知恵袋より)
読了時間: 約0分58秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「正弦定理から三角形の形状を考える」問題を解いてみました。
問題
三角形\( \ \mathrm{ABC} \ \)について
\(\Large \frac{\sin \mathrm{A}}{7}\)\( \ = \ \)\(\Large \frac{\sin \mathrm{B}}{6}\)\( \ = \ \)\(\Large \frac{\sin \mathrm{C}}{5}\)が成り立つとき、
三角形 \( \ \mathrm{ABC} \ \) は（ ① 鋭角 ② 鈍角 ③ 直角 ）三角形である。
\(\Large \frac{\sin \mathrm{A}}{7}\)\( \ = \ \)\(\Large \frac{\sin \mathrm{B}}{6}\)\( \ = \ \)\(\Large \frac{\sin \mathrm{C}}{5}\)が成り立つとき、
三角形 \( \ \mathrm{ABC} \ \) は（ ① 鋭角 ② 鈍角 ③ 直角 ）三角形である。
解法
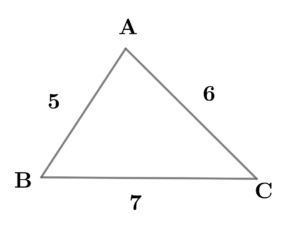\( \ a=7 \ \), \( \ b=6 \ \), \( \ c=5 \ \) として考える。最大辺の対角が最大角であるので、\( \ \angle \mathrm{A} \ \)の大きさを考える。
余弦定理より
$$\begin{align}\cos \angle \mathrm{A}=&\frac{b^2+c^2-a^2}{2bc} \\\\ =&\frac{36+25-49}{2\cdot 30} \\\\ =&\frac{1}{5} \gt 0 \end{align}$$ ゆえに \( \ \angle \mathrm{A} \ \) が鋭角であるから、
三角形\( \ \mathrm{ABC} \ \) は ① 鋭角三角形である。
こたえ
① 鋭角三角形
共有:
プロフィール
Author Profile
