外分を含む平面ベクトル（その1）【たすきがけで比を統一せよ!!】

2023年1月13日ベクトル実用数学技能検定（数学検定 数検),数検2級,数検準1級

「外分」でも「内分」と同じように。

Lukia

これまでの記事は、「内分比」を扱ってきました。
「外分比」は一見難しそうですが、ためしに「内分比」と同じように各頂点に比をおいてみたところ、特に問題は生じませんでした。
ちょっとコツはあるので、そこを説明します。

Lukia

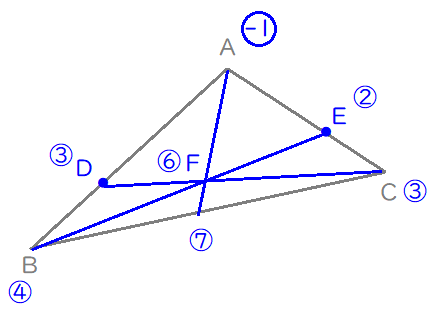
「辺\(\mathrm{AB}\)を\(4:1\)に外分する点\(\mathrm{D}\)」の打ち方と比の置き方です。
頂点\(\mathrm{B}\)の上に比の4（図では〇で囲んでいます）を書き、頂点\(\mathrm{A}\)には\(\color{#0004fc}{-1}\)を書きます。
本来、外分点\(\mathrm{D}\)は、線分\(\mathrm{AB}\)の延長線上にあり、3点は\(\mathrm{A, \ B, \ D}\)と並びます。
しかし、\(\color{#0004fc}{-}\)（マイナス）をつけて表すことで、「内分比」と同じように扱うことができるのです。
ゆえに点\(\mathrm{D}\)の比は、両端点の和である\(3\)となります。
同様に辺\(\mathrm{AC}\)を\(3:1\)に外分する点\(\mathrm{E}\)についても、頂点\(\mathrm{A}\)の上に書く比を\(\color{#0004fc}{-1}\)とおくことで、
内分点のように扱うことができます。

準備

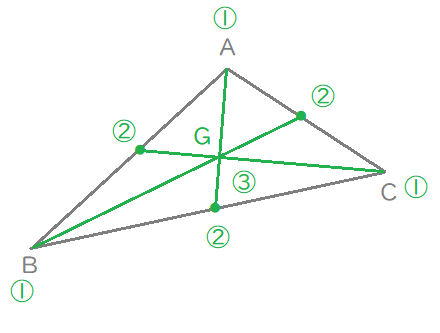
$$\begin{align}\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}=&\overrightarrow{0}\quad より, \\\\ \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=&\overrightarrow{0}\quad \cdots \ *\end{align}$$

(1)を解く。

ⅰ）
$$\begin{align}\overrightarrow{\mathrm{GD}}=&\overrightarrow{\mathrm{AD}}-\overrightarrow{\mathrm{AG}} \\\\ =&\displaystyle\frac{4}{3}\overrightarrow{\mathrm{AB}}+\overrightarrow{a} \\\\ =&\displaystyle\frac{1}{3}\left( 4\overrightarrow{b}-4\overrightarrow{a}+3\overrightarrow{a}\right)\\\\ =&-\displaystyle\frac{1}{3}\overrightarrow{a}+\displaystyle\frac{4}{3}\overrightarrow{b} \end{align}$$
ⅱ）
*より
$$\begin{align}\overrightarrow{c}=&-\overrightarrow{a}-\overrightarrow{b}\end{align}$$
ⅲ）
$$\begin{align}\overrightarrow{\mathrm{GF}}=&t\overrightarrow{\mathrm{GD}}+\left( 1-t\right)\overrightarrow{\mathrm{GC}} \\\\ =&\displaystyle\frac{1}{3}\lbrace -t\overrightarrow{a}+4t\overrightarrow{b}-3\left( 1-t\right)\overrightarrow{a}-3\left( 1-t\right)\overrightarrow{b}\rbrace \\\\ =&\displaystyle\frac{1}{3}\lbrace \left( 2t-3\right)\overrightarrow{a}+\left( 7t-3\right)\overrightarrow{b}\rbrace\\\\ =&\left( \displaystyle\frac{2}{3}t-1\right) \overrightarrow{a}+\left( \displaystyle\frac{7}{3}t-1\right)\overrightarrow{b}\quad \cdots \ ① \end{align}$$
ⅳ）
$$\begin{align}\overrightarrow{\mathrm{GF}}=&\left( 1-s\right)\overrightarrow{\mathrm{GB}}+s\overrightarrow{\mathrm{GE}} \\\\ =&\left( 1-s\right)\overrightarrow{b}+\displaystyle\frac{s}{2}\left( -\overrightarrow{a}+3\overrightarrow{c}\right) \\\\ =&\left( 1-s\right)\overrightarrow{b}+\displaystyle\frac{s}{2}\left( -4\overrightarrow{a}-3\overrightarrow{b}\right)\\\\ =&-2s\overrightarrow{a}+\left( 1-\displaystyle\frac{5}{2}s\right)\overrightarrow{b}\quad \cdots \ ②\end{align}$$
ⅴ）
①と②より
$$\begin{align}\displaystyle\frac{2}{3}t-1=&-2s \\\\ \displaystyle\frac{7}{3}t-1=&1-\displaystyle\frac{5}{2}s\\\\ \\\\連立方程式を解いて\\\\ &s=\displaystyle\frac{1}{3},\quad t=\displaystyle\frac{1}{2} \end{align}$$

(2)を解く。

条件より
$$\begin{align}\vert \overrightarrow{a} \vert:\vert \overrightarrow{\mathrm{GF}} \vert=& 3:2\\\\ 2\vert \overrightarrow{a} \vert=&3\vert \overrightarrow{\mathrm{GF}} \vert \\\\ 両辺を2乗して& \\\\ 4\vert \overrightarrow{a} \vert^2=&9\vert \overrightarrow{\mathrm{GF}} \vert^2 \\\\ =&9\vert -\displaystyle\frac{2}{3}\overrightarrow{a}+\displaystyle\frac{1}{6}\overrightarrow{b} \vert^2\\\\ =&4\vert \overrightarrow{a} \vert^2-2\overrightarrow{a}\cdot \overrightarrow{b}+\displaystyle\frac{1}{4}\\\\ \\\\ 2\overrightarrow{a}\cdot \overrightarrow{b}=&\displaystyle\frac{1}{4}\\\\ \overrightarrow{a}\cdot \overrightarrow{b}=&\displaystyle\frac{1}{8}\end{align}$$

こたえ

平面ベクトル三角形の内分点 記事一覧【たすきがけで比を統一せよ!!】

平面ベクトルの習い始めによく演習する「三角形の内分点」に関する問題を集めました。一見難しそうな外 ...

 https://makelemonadejp.com/plane-vector-internal-division-of...

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。