高校数学の「絶対値がらみの三角関数の合成」に関する問題を解いてみる。(Yahoo!知恵袋より)
読了時間: 約2分58秒
[mathjax]
問題
\( \ y=\vert 1-\sin x+\sqrt{3}\cos x \vert \ \)の
\( \ 0 \leq x \lt \pi \ \) における値域を求めよ。
\( \ 0 \leq x \lt \pi \ \) における値域を求めよ。
解法
三角関数の合成
まずは、絶対値の中にある三角関数を合成してしまいましょう。
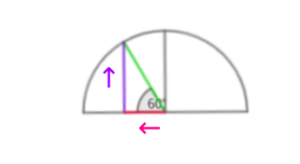
三角関数の合成の方法はいろいろあるのですが、
私の場合は、\( \ \sin x \ \)の係数\( \ −1 \ \)を横に、
\( \ \cos x \ \)の係数\( \ \sqrt{3} \ \)を縦とする直角三角形を作成し、
斜辺と横の半直線がなす角を求めています。
私の場合は、\( \ \sin x \ \)の係数\( \ −1 \ \)を横に、
\( \ \cos x \ \)の係数\( \ \sqrt{3} \ \)を縦とする直角三角形を作成し、
斜辺と横の半直線がなす角を求めています。
定義域から絶対値を考えずに値域を求める
定義域 \( \ 0 \leq x \lt \pi \ \) を変形して、
ひとまず絶対値を考えずに値域を求めてみます。
ひとまず絶対値を考えずに値域を求めてみます。
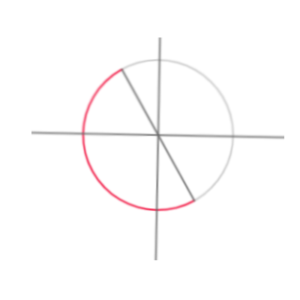
定義域は、上の図の赤い弧が示すところとなります。
この場合、最も大きい（高い）値をとるのは、 \( \ {\frac{ 2 }{ 3 }}\pi \ \)のとき。
最も小さい（低い）値をとるのは、\( \ {\frac{ 3 }{ 2 }}\pi \ \)のときですね。
この場合、最も大きい（高い）値をとるのは、 \( \ {\frac{ 2 }{ 3 }}\pi \ \)のとき。
最も小さい（低い）値をとるのは、\( \ {\frac{ 3 }{ 2 }}\pi \ \)のときですね。
ようやく絶対値を考える
絶対値とは、「\( \ 0 \ \)からの距離」ですから、 距離（大きさ）に負はありませんね。
（負は、方向を表していると考えるとよいでしょう）
絶対値を考えない場合は、\( \ -1 \leq 1+2\sin \left( x+{\frac{ 2 }{ 3 }}\pi\right) \leq 1+\sqrt{3} \ \)でよいのですが、
絶対値を考えるなら、\( \ −1 \ \)を\( \ 0 \ \)に直す必要がありますね。
（負は、方向を表していると考えるとよいでしょう）
絶対値を考えない場合は、\( \ -1 \leq 1+2\sin \left( x+{\frac{ 2 }{ 3 }}\pi\right) \leq 1+\sqrt{3} \ \)でよいのですが、
絶対値を考えるなら、\( \ −1 \ \)を\( \ 0 \ \)に直す必要がありますね。
\( \ \vert -1 \vert \ \)と\( \ \vert 1+\sqrt{3} \vert \ \)の大小比較をする。
$$\begin{align}\vert 1+\sqrt{3} \vert-\vert -1 \vert=&1+\sqrt{3}-1 \\\\ =&\sqrt{3} \\\\ \\\\ 1 \lt &\sqrt{3} \lt 2\quad より \\\\ \\\\ 明らかに&\sqrt{3} \gt 0\\\\ ゆえに&\vert 1+\sqrt{3} \vert \gt \vert -1 \vert \end{align}$$ ゆえに求める値域は $$0 \leq y \leq \sqrt{3}+1$$
本来、上記のような絶対値の大小比較をする必要はありません。
（暗算してもらえばいいだけです）
しかし、絶対値がない値域の最小値と最大値の大小関係がそのまま、絶対値の大小関係になるとは限りませんので、頭の中で大小比較をしてください。
最小値がめちゃくちゃ小さい場合、最小値と0との距離（絶対値）が、最大値と0との距離（絶対値）よりも大きい場合がありますからね。
（暗算してもらえばいいだけです）
しかし、絶対値がない値域の最小値と最大値の大小関係がそのまま、絶対値の大小関係になるとは限りませんので、頭の中で大小比較をしてください。
最小値がめちゃくちゃ小さい場合、最小値と0との距離（絶対値）が、最大値と0との距離（絶対値）よりも大きい場合がありますからね。
こたえ
$$0 \leq y \leq \sqrt{3}+1$$共有:
プロフィール
Author Profile