高校数学の「平面ベクトル・点の存在範囲」に関する問題を解いてみる。(Yahoo!知恵袋より)

読了時間: 約2分16秒
問題
[mathjax]
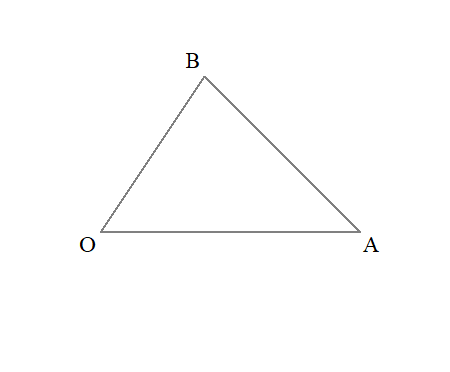
\( \ \mathrm{O}\left( 2 \ , \ 3 \right) \ , \ \mathrm{A}\left( 5 \ , \ 0 \right) \ , \ \mathrm{B}\left( 2 \ , \ 3\right) \ \)に対して、点\( \ \mathrm{P} \ \)が\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ , \ 0 \leq 2s+t \leq 2 \ , \ s \geq 0 \ , \ t \geq 0\ \)を満たしながら動くとき、
点\( \ \mathrm{P}\ \)の存在範囲を図示せよ。
解法

\( \ 0 \leq 2s+t \leq 2\ \)を操作して、右端の2を1にすること。
sまたはt(ときには両方のこともあります)を新たな文字に置き換えるということをやっていきましょう。
sまたはt(ときには両方のこともあります)を新たな文字に置き換えるということをやっていきましょう。
\( \ 0 \leq 2s+t \leq 2 \ \)の各辺を2で割ると
\( \ 0 \leq s+\frac{1}{2}t \leq 1 \ \)と表せる。
また
\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}\ \) は、
\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+\frac{1}{2}t\cdot 2\overrightarrow{\mathrm{OB}}\ \) と表せる。
ここで、
\( \ \frac{1}{2}t=k \ \)とする。(\( \ k \geq 0 \ \)を満たす)
\( \ 2\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OB’}}\ \)とすると、
与式は
\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+k\overrightarrow{\mathrm{OB’}} \ \)
\( \ 0 \leq s+k \leq 1 \ , \ s \geq 0 \ , \ k \geq 0 \ \)

sとkは、言い換えると、それぞれ0以上1以下の範囲で動くことができます。
これは、たとえば、s=0かつk=0でもいいし、(点O)
s=0かつk=1でもいいし、(点B’)
s=1かつk=0でもいいわけです。(点A)
そして、s+k=1を満たしてもいい。(線分AB’上)
動ける限界はこの線分AB’上までで、この線分の向こう側(点Oの反対側)には存在できません。
これは、たとえば、s=0かつk=0でもいいし、(点O)
s=0かつk=1でもいいし、(点B’)
s=1かつk=0でもいいわけです。(点A)
そして、s+k=1を満たしてもいい。(線分AB’上)
動ける限界はこの線分AB’上までで、この線分の向こう側(点Oの反対側)には存在できません。
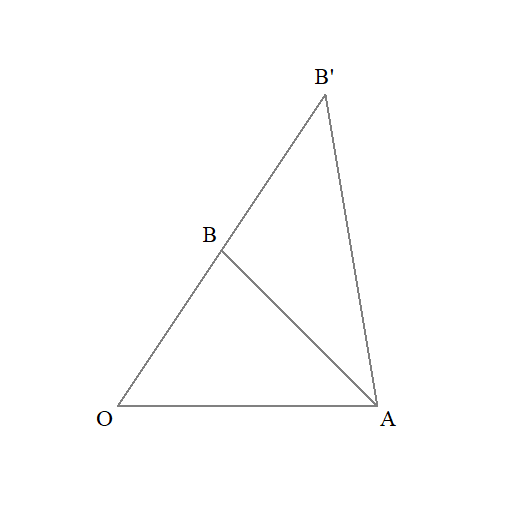
こたえ
点\( \ \mathrm{P} \ \)は、\( \ \triangle \mathrm{OAB’} \ \)の周上とその内部に存在する。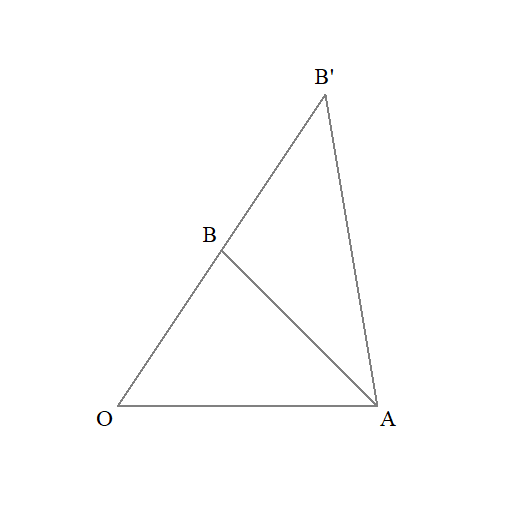
[subscribe2]









ディスカッション
コメント一覧
まだ、コメントがありません