高校数学の「二次関数の平行移動」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年10月15日2023年1月15日二次関数実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

二次関数は軸と頂点をビンビン意識せよ！

Lukia

二次関数の平行移動は、センター試験出題者の大好物です。
引っかかり、パニくる受験生を手ぐすね引いて待っているのです。
しかし、問題を解き始める際に、必ず、軸と頂点を明らかにしておく。という習慣をつけておけば、
結構簡単に解けるようになる問題でもあります。

$$\begin{align}y=&x^2-6x+2 \\\\ =&\left( x-3\right)^2-9+2 \\\\=&\left( x-3\right)^2-7 \end{align}$$
ゆえに、頂点は、
$$\left( 3　,　-7\right)$$

頂点を平行移動させる。

$$\begin{align}求める放物線の方程式は、& \\\\ x軸方向に&a \\\\ y軸方向に&b　平行移動したものと考える。\\\\&\left( ただし、aとbは実数\right) \end{align}$$
これより、求める放物線の方程式は、
$$\begin{align}y\color{blue}{-b}=&\left( x-3\color{blue}{-a}\right)^2-7 \\\\すなわち、& \\\\ y=&\left( x-3\color{blue}{-a}\right)^2-7\color{blue}{+b} \cdots ☆ 　とあらわせる。\end{align}$$

代入して連立方程式を解く。

Lukia

☆に2つの座標を代入して、aとbに関する連立方程式を解きます。

$$\begin{align}☆に\left( -1　,　6\right)を&代入して、 \\\\ 6=&\left( -4-a\right)^2-7+b \cdots ① \end{align}$$
$$\begin{align}☆に\left( 2　,　3\right)を&代入して、 \\\\ 3=&\left( -1-a\right)^2-7+b \cdots ② \end{align}$$
$$\begin{align}①-②を&行う。 \\\\ 3=&\left( -4-a\right)^2-\left( -1-a\right)^2\\\\3=&\left( -4-a-1-a\right)\left( -4-a+1+a\right) \\\\3=&3\left( 2a+5\right) \\\\1=&2a+5\\\\ a=&-2 \end{align}$$
$$\begin{align}a=-2を&①に代入して、 \\\\ 6=&\left( -4+2\right)^2-7+b \\\\ b=&9 \end{align}$$

Lukia

つまり、求める放物線は、
\(y=x^2-6x+2\)を、
\(x\)軸方向に\(-2\)　,　\(y\)軸方向に\(9\) 平行移動させたものとわかります。

$$\begin{align}a=-2　,　b=9&を☆に代入して、 \\\\ y=&\left( x-3+2\right)^2-7+9 \\\\ y=&\left( x-1\right)^2+2\\\\ y=&x^2-2x+3 \end{align}$$

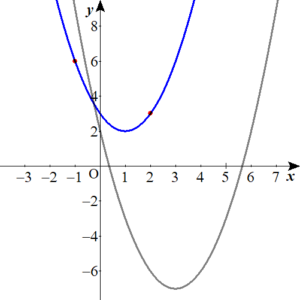
イメージ

Lukia

以下のグラフで、平行移動を具体的にイメージしてみましょう。
灰色の放物線が、もとの\(y=x^2-6x+2\) です。
そして、青い放物線が、平行移動後の\(\color{blue}{y=x^2-2x+3}\)です。
青い放物線上の二つの赤い点は、それぞれ、\(\color{red}{\left( -1　,　6\right)}\) , \(\color{red}{\left( 2　,　3\right)}\)です。

こたえ

$$\Large y=x^2-2x+3 $$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。