数学検定準1級の「y軸回転」問題を解いてみる。
2018年7月22日実施の
第322回「実用数学技能検定（以下数検）」の受検にむけ、
問題
$$\begin{align} xy 平面上の曲線 y=\frac{x}{\sqrt{1+x^2}} \left( 0 \leq x \leq 1\right)と y 軸、\ 直線y=\frac{1}{\sqrt{2}} で囲まれた図形を、\ y 軸の周りに1回転させてできる立体の体積\rm{V} を求めよ。\end{align}$$
目標
$$\Large V=\pi\int_0^{\frac{1}{\sqrt{2}}} x^2 dy$$
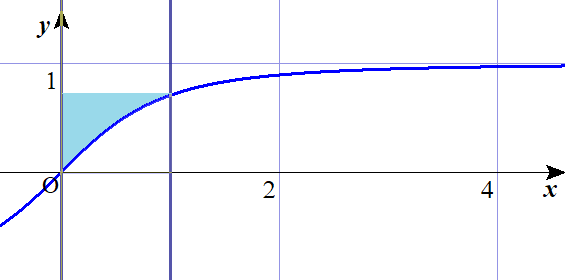
逆関数を求める。
Lukia
\(\Large f\left( g\left( x\right)\right)=x\) を利用して逆関数を求めます。
$$\Large \begin{align}f\left( y\right)&=x より、 \ \frac{y}{\sqrt{1+x^2}}&=x \両辺を2乗して、\ y^2&=x^2\left( 1+y^2\right) \ -x^2&=\left( x^2-1\right)y^2 \y^2&=\frac{-x^2}{x^2-1}
より、\ x^2&=\frac{-y^2}{y^2-1} \end{align}$$
式を計算していく。
$$\Large \begin{align} \frac{V}{\pi}&=\int_0^{\frac{1}{\sqrt{2}}} \frac{-y^2}{y^2-1} dy \ \color{red}{-}\frac{V}{\pi}&=\int_0^{\frac{1}{\sqrt{2}}} \frac{y^2}{y^2-1} dy \ &=\int_0^{\frac{1}{\sqrt{2}}} \frac{\color{red}{\left( y^2-1\right)+1}}{y^2-1} dy \ &=\left[y\right]_0^{\frac{1}{\sqrt{2}}}+\int_0^{\frac{1}{\sqrt{2}}} \frac{1}{y^2-1} dy \end{align}$$
なんなら、覚えちゃえ！
$$\Large \int_\beta^\alpha \frac{1}{x^2-1} dx=\frac{1}{2}\left[\log \frac{\vert x-1 \vert}{x+1}\right]_\beta^\alpha$$
計算にもどります。
$$\Large \begin{align} \frac{-V}{\pi}&=\frac{1}{\sqrt{2}}+\frac{1}{2}\left[\log \frac{\vert y-1 \vert}{y+1}\right]_0^{\frac{1}{\sqrt{2}}}\ &=\frac{1}{\sqrt{2}} +\frac{1}{2}\log \left( \sqrt{2}-1\right)^2 \ &=\frac{1}{\sqrt{2}} +\log \left( \sqrt{2}-1\right) \ V&=-\pi \log \left( \sqrt{2}-1\right)-\frac{\sqrt{2}}{2}\pi \end{align}$$
ポイント
$$\Large \begin{align}&\int の周りはシンプルな状態を保つ。\ & （不急の文字や数字は移項して、計算に集中する）\end{align}$$
$$\Large 分数の分子を1や \left(分母\right)’ の形にして対数（log）にもちこむ。$$
