高校数学の「四角形の計量」に関する問題を解いてみる。(Yahoo!知恵袋より)

[mathjax]
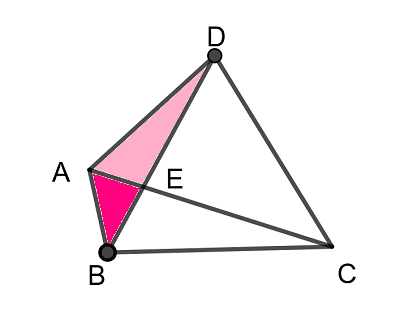
\( \ \mathrm{AB}=1 \ , \ \mathrm{AD}=2 \ , \ \mathrm{AC}=3 \ , \ \mathrm{BC}=\mathrm{BD}=\sqrt{7} \ \)とする.\( \ \mathrm{AC} \ \)と\( \ \mathrm{BD} \ \)の交点を\( \ \mathrm{E} \ \)とおくとき,次の問いに答えよ.
(1) \( \ \angle \mathrm{BAC} \ \)と\( \ \angle \mathrm{CAD} \ \)を求めよ。
(2) 辺\( \ \mathrm{CD} \ \)の長さを求めよ。
(3) 線分\( \ \mathrm{BE} \ \)の長さを求めよ。
(4) 線分\( \ \mathrm{AE} \ \)の長さを求めよ。
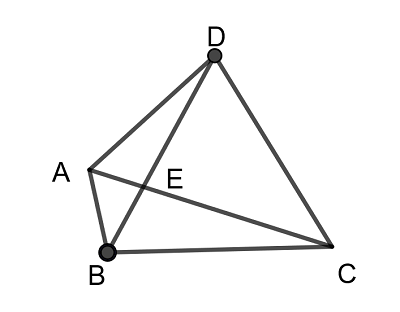
三角形ABCをもとに(1)を求める。
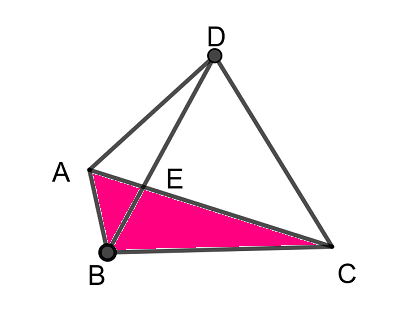
$$\begin{align}\triangle \mathrm{ABC}\quad &において余弦定理より \\\\ \cos \angle \mathrm{BAC}=&\frac{\mathrm{AB}^2+\mathrm{AC}^2-\mathrm{BC}^2}{2\mathrm{AB}\cdot \mathrm{AC}}=\frac{1}{2} \\\\ ゆえに\quad \angle \mathrm{BAC}=&60^{\circ} \end{align}$$
三角形ABDをもとに(1)を求める。
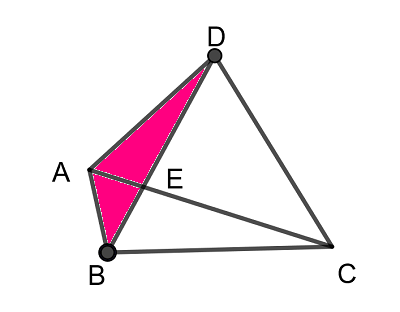
$$\begin{align}\triangle \mathrm{ABD}\quad &において余弦定理より \\\\ \cos \angle \mathrm{BAD}=&\frac{\mathrm{AB}^2+\mathrm{AD}^2-\mathrm{BD}^2}{2\mathrm{AB}\cdot \mathrm{AD}}=-\frac{1}{2} \\\\ ゆえに\quad \angle \mathrm{BAD}=&120^{\circ}\\\\ \ \angle \mathrm{BAD}=&\angle \mathrm{BAC}+\angle \mathrm{CAD}\quad より\\\\ \angle \mathrm{CAD}=&60^{\circ} \end{align}$$
三角形ACDをもとに(2)を求める。
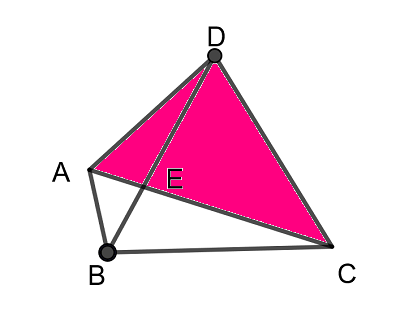
$$\begin{align}\triangle \mathrm{ACD}\quad &において余弦定理より \\\\ \cos \angle \mathrm{CAD}=&\frac{\mathrm{AC}^2+\mathrm{AD}^2-\mathrm{CD}^2}{2\mathrm{AC}\cdot \mathrm{AD}}\\\\ \mathrm{CD}^2=&7\\\\ \mathrm{CD} \gt &0\quad より\quad \mathrm{CD}=\sqrt{7} \end{align}$$
再び三角形ABDをもとに(3)を求める。

$$\begin{align}線分\mathrm{AE}は&\angle \mathrm{BAD} \ の二等分線であるから, \\\\ \mathrm{BE}:\mathrm{ED}=&\mathrm{AB}:\mathrm{AD}=1:2 \\\\ \mathrm{BE}=&\frac{1}{3}\mathrm{BD}\quad より\\\\ \mathrm{BE}=&\frac{\sqrt{7}}{3} \end{align}$$
(3)をもとに(4)を求める。
$$\begin{align}\triangle \mathrm{ABE}=&\frac{1}{3}\triangle \mathrm{ABD}\quad である. \\\\ \frac{1}{2}\times \mathrm{AE}\times \mathrm{AB}\times \sin 60^{\circ}=&\frac{1}{3}\times \frac{1}{2}\times \mathrm{AB}\times \mathrm{AD}\times \sin 60^{\circ}\\\\ \mathrm{AE}=&\frac{2}{3} \end{align}$$

Lukia
まずは式をしっかり立てて、計算はできるだけ最後の最後まで取っておきましょう。

Lukia
\( \ \triangle \mathrm{ABE} \ \)について余弦定理を用いることはできます。
しかし、計算すると、線分\( \ \mathrm{AE} \ \)の値は\( \ \frac{2}{3} \ \)または\( \ \frac{1}{3} \ \)が出てきてしまい、
どちらかにしぼる決め手がありません。(二乗が含まれると、こういう厄介ごとが生じるんですね。)
ゆえに、線分比から面積比にシフトし、辺\( \ \mathrm{AE} \ \)の長さそのものを求める式を立てていきます。

Lukia
もしかして、面積を求めることで、アプローチできる?)などと、疑ってみるのも解法のテクニックのひとつです。










ディスカッション
コメント一覧
まだ、コメントがありません