高校数学の「三角関数の最小値」に関する問題を解いてみる。（Yahoo!知恵袋より）
読了時間: 約1分23秒
問題
[mathjax]\( \ y=-12\sin \theta+5\cos \theta+3 \ \)の最小値を求めよ。
解法
Lukia
あらかじめおことわりしておくことがあります。
不等号（＜）の下に等号（=）がついている「小なりイコール」がうまく表示されないため、
不等号の下に一本線の「小なりイコール」にて対応させています。
（意味は同じです）
不等号（＜）の下に等号（=）がついている「小なりイコール」がうまく表示されないため、
不等号の下に一本線の「小なりイコール」にて対応させています。
（意味は同じです）
[mathjax]
\( \ \begin{align}与式=&\sqrt{\left( −12\right)^2+5^2}\sin \left( \theta+\alpha\right)+3 \\ &\left( ただし\alpha \ は\quad \sin \alpha=\frac{5}{13} \ , \ \cos \alpha=-\frac{12}{13} \ を満たす角\right) \end{align} \ \)
\begin{align}0 \leq &\theta \leq 2\pi \\ \alpha \leq &\theta+\alpha \leq 2\pi+\alpha \\ -1 \leq &\sin \left( \theta+\alpha\right) \leq 1\\ -13 \leq &13\sin \left( \theta+\alpha\right) \leq 13\\ -13+3 \leq &13\sin \left( \theta+\alpha\right)+3 \leq 13+3\\ -10 \leq &y \leq 16 \end{align}
\( \ ゆえに最小値は \ −10 \ \)
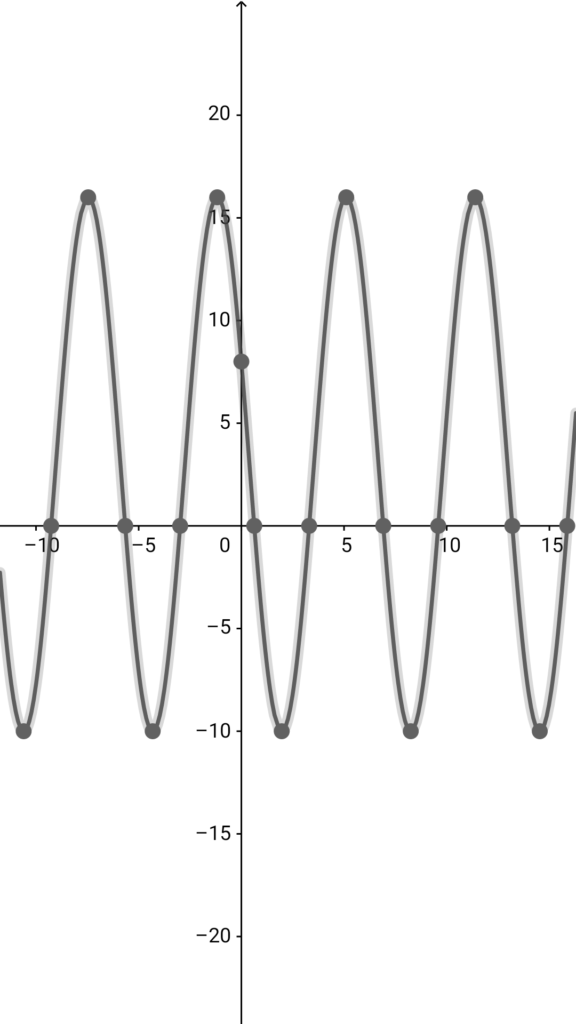
グラフも描いてみました
Lukia
\( \ y=-12\sin \theta+5\cos \theta+3 \ \)のグラフをGeoGebra（ジオジブラ）を使って描いてみました。今回求めるのは、最小値でしたね。
こたえ
$$-10$$
共有:
プロフィール
Author Profile