高校数学の「三角比や辺の長さ」に関する問題を解いてみる。（Yahoo!知恵袋より）

2020年5月7日2023年1月13日図形と計量実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

Lukia

 2020年のゴールデンウィーク的なものも終わりましたね。 一本もブログを書かずに、休みを終えてなるものか！と、記事をあげようと思います。 （ネタノートだけはパンパンです）

不正確でも描かないよりはマシ。

Lukia

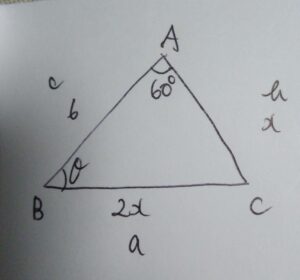
 図形の問題を解くときは、とにかく問題文の「文字情報」を、図形という「視覚的情報」に変換する作業に力を入れることが大切です。 はじめからかなり正確な図形が描けるにこしたことはないのですが、高校数学の場合、計算によって数値を求めることが主なので、かなりアバウトなものでかまいません。 実際、私の描いた図もこの程度です。 辺\( \ a \ \)と辺\( \ b \ \)の比は\( \ 2：1 \ \)のはずなのに、ほとんど反映されていないでしょ？(笑) はじめはこの程度でいいんです。 問題が進むにつれ、たとえフリーハンドでももう少し正確な図を描いた方が解きやすくなるという問題はありますが、 今回は、このぐらいアバウトで十分です。 もっともやっちゃだめなのは、図形の問題なのに、一切図を描かないこと。 「不正確でも描かないよりはマシ！」と開き直って、ガシガシ描きましょう。

辺の長さを文字で置いたっていい

Lukia

このタイトル、ぺこぱの松蔭寺さん風に読んでもらえればうれしいです。(笑) 数学は、正確な数値がわからない場合、文字を置きます。 ある意味、「わからない。」ってことを明確にするために文字で表現するんですね。 今回、（2）の問題で辺\( \ b \ \)の長さを求めるので、\( \ b=x \ \)と置きます。 さらに、\( \ x \ \)は「辺の長さ」を示すので、\( \ x \gt 0 \ \)という条件も必要ですね。 問題を解く私たちには、「正確な数値のわからないものを文字に置く」という自由が与えられていますが、 「置いた文字が何を表すのかきちんと説明する、なんなら条件も付け加えておく」という責任なり義務なりも課せられています。 単にテクニックを覚えるだけでなく、解法を読む相手がいることを意識すると、数学は徐々にできるようになるのではないかと思います。

(1)を解く

$$\begin{align}辺 \ b=&x\quad \left( ただし \ x \gt 0\right) とすると\\\\ a=&2x\quad と表せる. \\\\ 正弦定理より&\\\\ &\frac{a}{\sin \mathrm{A}}=\frac{b}{\sin \mathrm{B}}\\\\ & \sin \mathrm{B}=\frac{b\sin \mathrm{A}}{a}=\frac{x\cdot \frac{\sqrt{3}}{2}}{2x}=\frac{\sqrt{3}}{4} \end{align}$$

(2)を解く

Lukia

 せっかく辺\( \ c \ \)の長さが与えられているのですから、 余弦定理を用いて辺\( \ b \ \)の長さを求めましょう。 また、\( \ \cos 60^{\circ} \ \)の大きさは、暗記必須レベルですから、これを求める体ていで余弦定理を導けるといいですね。

余弦定理より
$$\begin{align}\cos \mathrm{A}=&\frac{b^2+c^2-a^2}{2bc} \\\\ =&\frac{36+x^2-4x^2}{12x} \\\\ \frac{1}{2}=&\frac{x^2-12}{-4x}\\\\ -2x=&x^2-12\\\\ \\\\ x^2+2x-12=&0\\\\ x=&-1 \pm \sqrt{13}\\\\ \\\\ ここで&x \gt 0\quad より\\\\ &x=-1+\sqrt{13} \\\\ ゆえに&\quad b=-1+\sqrt{13} \end{align}$$

こたえ

$$\begin{align}\left( 1\right)\quad &\frac{\sqrt{3}}{4} \\\\ \\\\ \left( 2\right)\quad &-1+\sqrt{13} \end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。