高校数学の「放物線の条件から定数を求める」問題を解いてみる。（Yahoo!知恵袋より）

2019年12月6日2023年1月13日二次関数実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

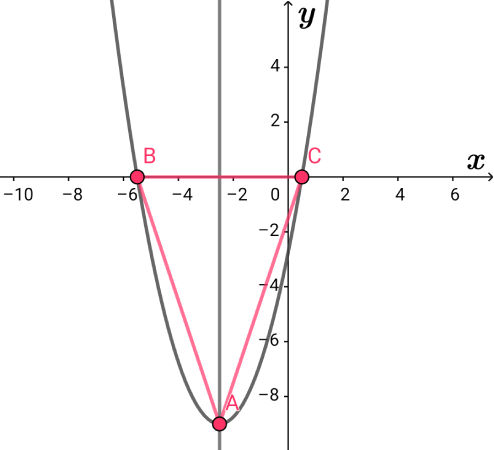
$$\begin{align}頂点\mathrm{A}が&\left( -\frac{5}{2} \ , \ a-\frac{25}{4}\right)\quad であることより \\\\ 放物線 \ p \ は \ y=&\left( x+\frac{5}{2}\right)^2+a-\frac{25}{4}\quad と表せる.\\\\ 放物線 \ p \ は&x軸と異なる2点で交わるから\\\\ a-\frac{25}{4} \lt &0\\\\ a \lt &\frac{25}{4}\quad である. \end{align}$$
$$\begin{align}\triangle \mathrm{ABC}の面積\mathrm{S}は& \\\\ \mathrm{S}=&\frac{1}{2}\sqrt{25-4a}\left( \frac{25}{4}-a\right) \\\\ =&\frac{1}{8}\sqrt{25-4a}\left( 25-4a\right)=27 \end{align}$$
式を変形する。
$$\begin{align}\sqrt{25-4a}\left( 25-4a\right)=&6^3\\\\ 両辺を&2乗する \\\\ \left( 25-4a\right)^3=&36^3 \\\\ \left( 25-4a\right)=&36 \end{align}$$
$$\begin{align}25-4a=&36 \\\\ -4a=&11 \\\\ a=&-\frac{11}{4}\quad \left( これは \ a \lt \frac{25}{4} \ を満たす\right) \end{align}$$

こたえ

$$a=-\frac{11}{4}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。