高校数学の「定数aを含む二次関数」に関する問題を解いてみる。（Yahoo!知恵袋より）
[mathjax]
\( \ f\left( x\right)=x^2-2ax+a+1 \ \) について考える.
(1) \( \ a=3 \ \)のとき,不等式\( \ f\left( x\right) \geq 0 \ \)を満たす\( \ x \ \)の範囲を求めよ.
(2) \( \ 0 \leq x \leq 2 \ \)における\( \ f\left( x\right) \ \)の最小値を\( \ m \ \)とする.\( \ a \ \)の値で場合分けして,\( \ m \ \)を求めよ.
(3) \( \ 0 \leq x \leq 2 \ \)を満たすすべての\( \ x \ \)に対して\( \ f\left( x\right) \geq 0 \ \)となるような\( \ a \ \)の値の範囲を求めよ.
（1）を解く。
$$\begin{align}a=3\quad &のとき, \\ f\left( x\right)=&x^2-6x+4=\left( x-3\right)^2-5\\ \\ \left( x-3\right)^2-5 \geq &0 \\ \left( x-3\right)^2 \geq &5\\ \\ x \leq &3-\sqrt{5}\quad ,\quad 3+\sqrt{5} \leq x \end{align}$$
（2）を解く。
$$\begin{align}f\left( x\right)=&\left( x-a\right)^2-a^2+a+1 \\ f\left( x\right)\quad &の最小値 \ m \ は,\\ &軸 \ x=a\quad と定義域の位置関係で定まり，以下の3通りが考えられる.\end{align}$$
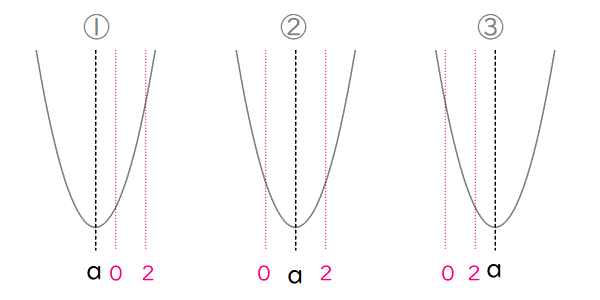
$$\begin{align}①\quad a \leq 0\quad のとき,\quad &m=f\left( 0\right)=a+1 \\ ②\quad 0 \lt a \lt 2\quad のとき,\quad &m=f\left( a\right)=-a^2+a+1 \\ ③\quad 2 \leq a\quad のとき,\quad &m=f\left( 2\right)=-3a+5 \end{align}$$
（3）を解く。
Lukia
ただし、①～③のいずれもが使えるのかどうかは、確かめてみなければなりません。
（2）より,
$$\begin{align}①\quad &a \leq 0\quad かつ\quad a+1 \geq 0 \\ &-1 \leq a \leq 0 \\\end{align}$$
$$\begin{align}②\quad &0 \lt a \lt 2\quad かつ\quad -a^2+a+1 \geq 0 \\ &0 \lt a \lt 2\quad かつ\quad \frac{1-\sqrt{5}}{2} \leq a \leq \frac{1+\sqrt{5}}{2} \\ ゆえに,\quad &0 \lt a \leq \frac{1+\sqrt{5}}{2}\end{align}$$
$$\begin{align}③\quad &2 \leq a\quad かつ\quad -3a+5 \geq 0 \\ すなわち,\quad &a \leq \frac{5}{3}\quad かつ\quad 2 \leq a \\ これを満たす&\quad a \ は存在しないので,不適. \end{align}$$
$$\begin{align}① \ , \ ② \ , \ ③より, & \\ &-1 \leq a \leq \frac{1+\sqrt{5}}{2} \end{align}$$
共有:
プロフィール
