高校数学の「絶対値を含んだ式の値域を求める」問題を解いてみる。（Yahoo!知恵袋より）

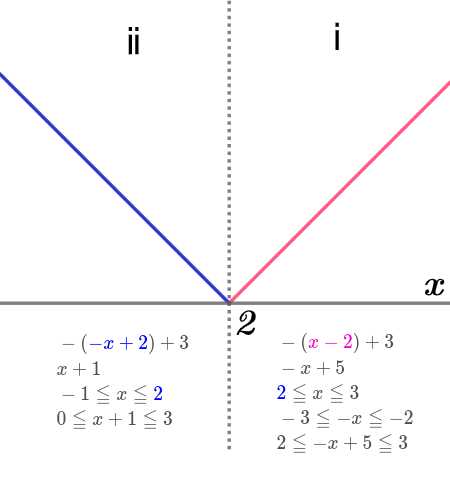
ⅰ）\( \ 2 \leq x \ \)のとき
$$\begin{align}y=&-\left( x-2\right)+3 \\\\ =&-x+5 \end{align}$$ ⅱ）\( \ x \lt 2 \ \)のとき
$$\begin{align}y=&-\left( -x+2\right)+3 \\\\ =&x+1 \end{align}$$

ⅰ）,ⅱ）より
定義域\( \ \left( -1 \leq x \leq 3\right) \ \)は、
新たに
ⅰ）
定義域\( \ \left( 2 \leq x \leq 3\right) \ \)と
ⅱ）
定義域\( \ \left( -1 \leq x \lt 2\right) \ \)に分けられる。


ⅰ）
$$\begin{align}2 \leq &x \leq 3 \\\\ -3 \leq &-x \leq -2 \\\\ 5-3 \leq &-x+5 \leq 5-2\\\\ 2 \leq &-x+5 \leq 3 \end{align}$$
ⅱ）
$$\begin{align}-1 \leq &x \lt 2 \\\\ 1-1 \leq &x+1 \lt 2+1 \\\\ 0 \leq &x+1 \lt 3 \end{align}$$ 以上より、求める値域は
\( \ \left( 0 \leq y \leq 3\right) \ \)