高校数学の「分数関数の逆関数」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年12月1日2023年1月13日平面上の曲線実用数学技能検定（数学検定 数検),数検準1級

式を変形して、シンプルな形にしよう。

Lukia

今、式は分母にも分子にも\( \ x \ \)が存在しています。分母の\( \ x \ \)は消すことはできないのですが、分子については工夫次第で消すことができます。
まずは、その操作をやってみましょう。

$$\begin{align}y=&f\left( x\right)\quad とする. \\\\ f\left( x\right)=&\frac{2-x}{x-1} \\\\ =&\frac{-\left( x-1\right)+1}{x-1} \\\\ =&\frac{1}{x-1}-1 \end{align}$$

Lukia

式\( \ \ \)をシンプルな形にすると、
漸近線ぜんきんせんがわかってきます。
漸近線は、曲線が限りなく近づくんだけど、交わることはないギリッギリの線のことです。
（数学的にはもっときっちりした表現があるのだろうと思いますが、イメージしてもらいやすいように話し言葉で書いています）

Lukia

\( \ f\left( x\right)=\frac{1}{x-\color{#0004fc}{1}}\color{#f700ca}{-1} \ \)より、
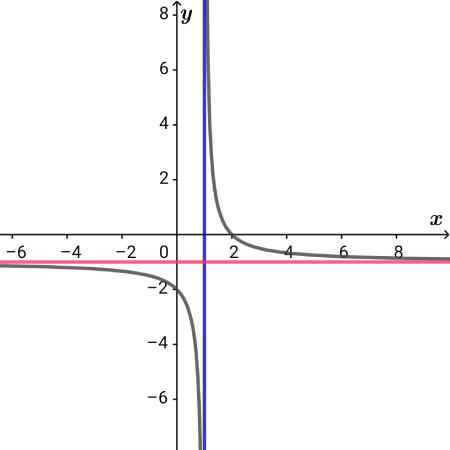
漸近線は、それぞれ\( \ x=\color{#0004fc}{1} \ , \ y=\color{#f700ca}{-1} \ \)とわかります。
以下が\( \ f\left( x\right) \ \)のグラフです。

Lukia

グラフに対して、曲線や漸近線が太いので、交わっているように見えますが、お互いにギリギリのところで交わらずに延々と伸びていきます。

Lukia

さらに、定義域が\( \ \left( x \lt 1\right) \ \)とありますので、下のグラフのように青い漸近線より左側の曲線だけが残ります。

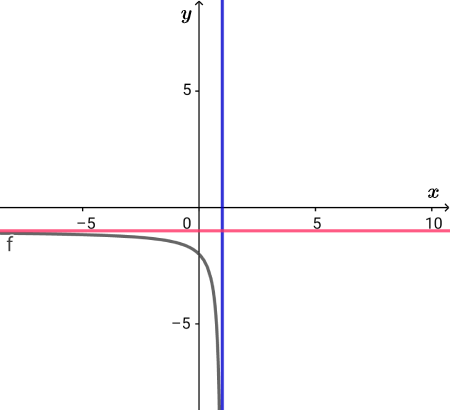
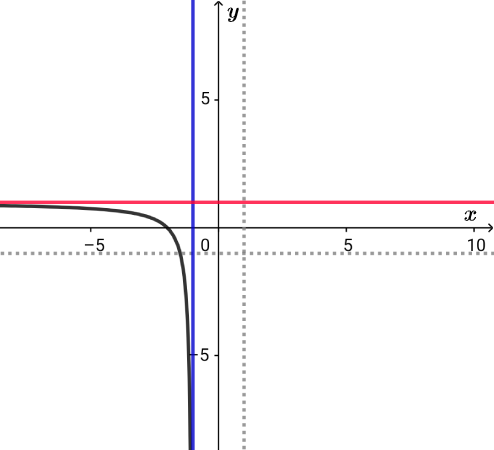
$$\begin{align}f\left( x\right)=&\frac{1}{x-1}-1\quad \left( x \lt 1\right) \\\\ グラフより&値域は \ y \lt -1 \end{align}$$

逆関数はy=xに関して対称であることを利用する

Lukia

逆関数は\( \ y=x \ \)に関して対称です。
それを利用して解いていきます。

$$\begin{align}f\left( x\right)の&逆関数を \ g\left( x\right) \ とする. \\\\ &\left( f\left( x\right)^{-1}=g\left( x\right)\right) \\\\ f\left( g\left( x\right)\right)=&x\\\\ \frac{1}{g\left( x\right)-1}-1=&x\quad \left( ただし,g\left( x\right) \neq 1\right)\\\\ \frac{1}{g\left( x\right)-1}=&x+1\\\\ g\left( x\right)-1=&\frac{1}{x+1}\\\\ g\left( x\right)=&\frac{1}{x+1}+1\quad 定義域は \ x \lt -1 \ \\\\ 以上より&求める逆関数は\\\\ y=&\frac{1}{x+1}+1\quad \left( x \lt -1\right) \end{align}$$

Lukia

問題の形式と合わせて、\( \ y=\frac{1}{x+1}+1 \ \)を
\( \ y=\frac{x+2}{x+1} \ \)と書き直しても問題ありません。

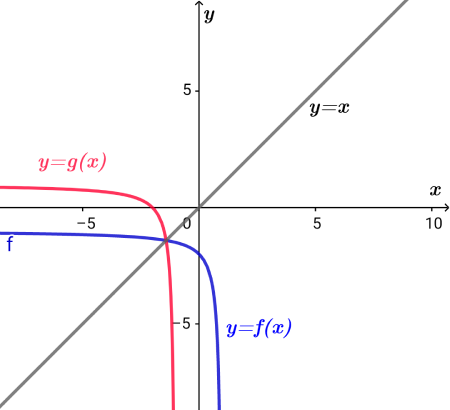
逆関数の関係性をグラフで確かめる

Lukia

以下に示すグラフで、逆関数が\( \ y=x \ \)に関して互いに対称となっていることを確認しておいてください。
ちなみに、青い曲線が\( \ \color{#0004fc}{y=f\left( x\right)} \ \)で、
ピンクの曲線が\( \ \color{#f700ca}{y=g\left( x\right)} \ \)です。

こたえ

$$y=\frac{x+2}{x+1}\quad \left( x \lt -1\right)$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。