高校数学の「放物線の各項の定数を求める」問題を解いてみる。(Yahoo!知恵袋より)

[mathjax]
解法
放物線は上に凸 すなわち \( \ a \lt 0 \ \) である必要がある。
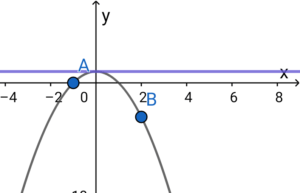
放物線の式に点\( \ \mathrm{A} \ \) , 点\( \ \mathrm{B} \ \)の値をそれぞれ代入する.
\( \ a-b+c=0 \ \cdots \ ① \ \)
\( \ 4a+2b+c=-3 \ \cdots \ ② \ \)
①\( \ \times 2+ \ \)②より
\( \ 2a+c=-1 \ \)
変形して、\( \ c=-1-2a \ \)
また①より
\( \ b=a+c=-a-1 \ \)
放物線と直線 \( \ y=1 \ \) が1つの共有点をもつとき、
\( \ ax^2+bx+c-1=0 \ \)が成り立つ。
この2次方程式の判別式を\( \ \mathrm{D} \ \)とすると、
$$\begin{align}\mathrm{D}=&b^2-4a\left( c-1\right)=0 \\\\
=&\left( -a-1\right)^2-4a\left( -1-2a-1\right)=0 \\\\
=&9a^2+10a+1=0\\\\
=&\left( a+1\right)\left( 9a+1\right)=0\\\\
a=&1 \ , \ a=-\frac{1}{9} \end{align}$$
2つの解はいずれも \( \ a \lt 0 \ \) を満たすので、放物線は2つあると推定できる。
ⅰ)\( \ a=-1 \ \) のとき
\( \ b=-a-1=0 \ \)
\( \ c=-1-2a=-1+2=1 \ \)
ゆえに求める放物線は \( \ y=-x^2+1 \ \)
ⅱ)\( \ a=- \ \)\(\Large \frac{1}{9}\) のとき
\( \ b=- \ \)\(\Large \frac{8}{9}\)
\( \ c=- \ \)\(\Large \frac{7}{9}\)
ゆえに求める放物線は \( \ y=- \ \)\(\Large \frac{1}{9}\)\( \ \left( x^2+8x+7\right) \ \)
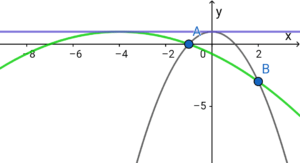
こたえ
\( \ y=- \ \)\(\Large \frac{1}{9}\)\( \ \left( x^2+8x+7\right) \ \)
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません