高校数学の「三角形の外接円・内接円の半径」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年8月24日2020年8月31日図形の性質Yahoo!知恵袋,数学,数学検定,数検準2級

問題

\( \ \triangle \mathrm{ABC} \ \)について\( \ a=8 \ , \ b=5 \ , \ c=7 \ \)であるとき、
\( \ \triangle \mathrm{ABC} \ \)の外接円の半径\( \ \mathrm{R} \ \)と内接円の半径\( \ r \ \)をそれぞれ求めよ。

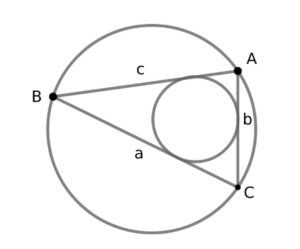
三角形の面積を3通り表現してみる。

Lukia

三角形の三辺の長さがわかっていて、ある角の大きさが知りたいならば、余弦定理を用いるべきでしょうが、
今回は、外接円、または内接円の半径の長さなので、余弦定理から攻めるルートだと、遠回りになってしまう可能性があります。
せっかく三辺の長さがわかっているので、「ヘロンの公式」を用いて、三角形の面積から、それぞれの半径の長さを求めてみましょう。

ヘロンの公式

$$\begin{align}\triangle \mathrm{ABC}&の面積を\mathrm{S}とする。\ s=&\frac{8+5+7}{2}=10\quad より\ \mathrm{S}=&\sqrt{10\cdot 2\cdot 5\cdot 3} =10\sqrt{3} \end{align}$$

内接円の半径を利用して

$$\begin{align}\mathrm{S}=&\frac{1}{2}r\left( a+b+c\right) \ \mathrm{S}=&r \frac{\left( a+b+c\right)}{2}=rs \ 10\sqrt{3}=&10r\ r=&\sqrt{3} \end{align}$$

外接円の半径と正弦定理を利用して

$$\begin{align}\angle \mathrm{BAC}=&\theta\quad とする。\ \mathrm{S}=&\frac{1}{2}bc\sin \theta \ \ 正弦定理より&\quad \mathrm{2R}=\frac{a}{\sin \theta} \ 辺々かけ& 合わせて\ \mathrm{2RS}=&\frac{1}{2}abc\ 4\mathrm{RS}=&abc\ 4\times 10\sqrt{3}\mathrm{R}=&8\times 5\times 7\ \mathrm{R}=&\frac{7\sqrt{3}}{3} \end{align}$$

式変形をして楽に計算しよう。

Lukia

いかがですか？
ヘロンの公式を知っていると、
\( \ \angle \mathrm{BAC}=\theta \ \)を具体的に求めずに、内接円や外接円の半径が求められるんですね。

Lukia

ヘロンの公式を知らない、または忘れている場合は、余弦定理から攻めるルートを取ることになります。
余弦定理は、使いこなせばすごい威力を発揮するんですが、
計算力やスピードが求められますので、リスクも伴うんですね。

Lukia

今回は、三角形の面積が幾通りもの求め方があることを利用して、内接円、外接円の半径を求めました。
\( \ \mathrm{S}=rs \ \)と\( \ 4\mathrm{RS}=abc \ \)を覚えておくと便利そうですね。

こたえ

$$\begin{align}外接円の半径 \ \mathrm{R}=&\frac{7\sqrt{3}}{3} \ \内接円の半径 \ r=&\sqrt{3} \end{align}$$

プロフィール

Author Profile

広島育ち・てんびん座。2018年末に潜伏先が福岡から広島になりました。
グレープフルーツとお好み焼きが大好きな元・再受験生。
現在は、数学関連の資格を取ろうと暗躍中。