高校数学の「定義域を定めて値を求める」問題を解いてみる。（Yahoo!知恵袋より）

2019年11月27日2023年1月13日数と式実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

ディノ

\( \ y= \ \)ほにゃららを取る\( \ x \ \)の値ってのは、これまでもやったことあるけど、
逆は初めてかもな。

Lukia

なんですか！絶対値の問題には、なんか特有の匂いでもあるんですか？

ディノ

別にないよ。ただ、気配は感じるかな〜。

Lukia

私、なにかストレス臭でも出しているんでしょうか。（汗）
（気を取り直し）
では、解いてみますかね。

定義域ごとの式を求める

ディノ

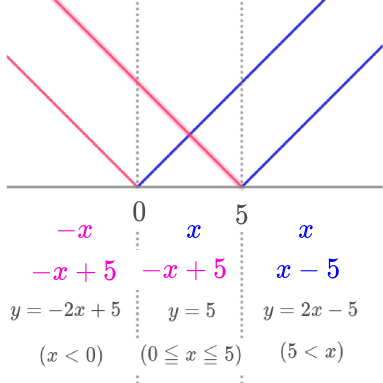
正確でなくていい、ざっくりしたものでいいから、直線のグラフを描く。
すると、こうなるな。

Lukia

うおぉ、はやっ！
数学の記事なのに、図とやり取りしか書いていませんから、ちょっと数学らしくまとめましょう。

$$\begin{align}y=&\vert x \vert+\vert x-5 \vert\quad は以下の3通りに書き分けられる. \\\\ y=&-2x+5\quad \left( x \lt 0\right) \quad \cdots\quad ①\\\\ y=&5\quad \left( 0 \leq x \leq 5\right)\quad \cdots\quad ② \\\\ y=&2x-5\quad \left( 5 \lt x\right) \quad \cdots\quad ③ \end{align}$$

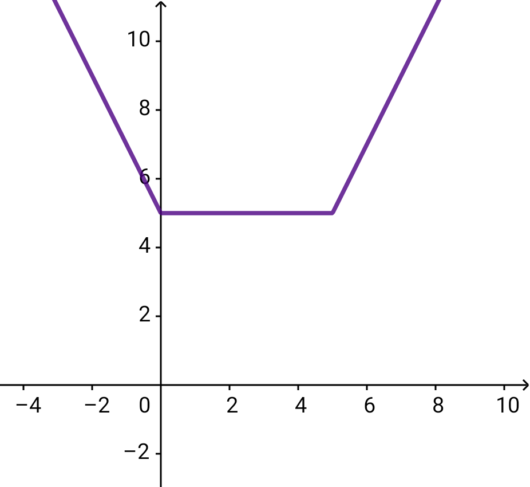
ルート3はどの定義域に含まれるの？

Lukia

ディノさん、\( \ \sqrt{3} \ \)のゴロ、覚えていますか？

ディノ

\( \ \sqrt{3} \ \)のゴロ？
ああ、中学校で覚えたヤツだよな。
フジサンロクニハトガナクだったっけ？

Lukia

ほぉ〜、富士山のふもとに鳩がいて、
平和に鳴いてますね〜、ぽろっぽ〜！って？
富士山麓が\( \ 2.236 \ \)ですから、
\( \ \sqrt{3} \ \)が\( \ 2 \ \)すなわち\( \ \sqrt{4} \ \)より大きいことになってしまいます。(笑)
それに鳴くのは鳩じゃなくて、オウムですよ？

ディノ

え〜、じゃ、なんだったけな。

Lukia

まず、ディノさんがいろいろ面白い間違いをしているのは、\( \ \sqrt{5} \ \)のゴロですね。
富士山麓オウム鳴く（\( \ 2.2360679 \ \)）と覚えます。

Lukia

\( \ \sqrt{3} \ \)のゴロは、
「人並みにおごれや」（\( \ 1.7320508 \ \)）です。

ぷくく・・・鳩って・・・。

ディノ

ふんっ、オレだって間違うことはあるさっ。（汗）

Lukia

ま、こんだけド派手に間違えれば、もう忘れませんね。(笑)
さて。話を戻しましょう。
今、ゴロで、\( \ \sqrt{3} \ \)がおおよそ\( \ 1.73 \ \)とわかりました。
これを数学チックに表して、答えを求めていきましょう。

$$\begin{align}\sqrt{3}& \ は\quad 1 \lt \sqrt{3} \lt 2\quad であるから,\\\\ 定義域が&0 \leq x \leq 5 \ の式②が該当する. \\\\ ゆえに&求める値は\quad 5 \end{align}$$

Lukia

ちなみに、\( \ x=\sqrt{3} \ \)を加えたグラフで確かめてみましょう。

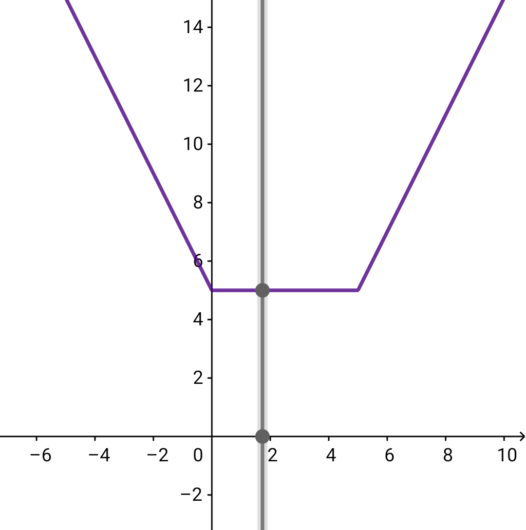
こたえ

$$5$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。