2019年大学入試センター試験数学1A「第2問図形と計量」を解いてみる。

2019年1月26日2023年1月14日図形と計量,大学入試センター試験実用数学技能検定（数学検定数検),数検準2級

読了時間: 約4分14秒

[mathjax]

問題

$ \ \triangle \mathrm{ABC} \ $において,$ \ \mathrm{AB}=3 \ , \ \mathrm{BC}=4 \ , \ \mathrm{AC}=2 \ $とする。

$ \ \cos \angle \mathrm{BAC}=\color{#0004fc}{\frac{アイ}{ウ}} \ $　であり,$ \ \angle \mathrm{BAC} \ $は$ \ \color{#0004fc}{エ} \ $である。
また,$ \ \sin \angle \mathrm{BAC}=\color{#0004fc}{\frac{\sqrt{オカ}}{キ}} \ $　である。

余弦定理より
$$\begin{align}\cos \angle \mathrm{BAC}=\frac{3^2+2^2-4^2}{2\cdot 3\cdot 2}=&\color{#0004fc}{\frac{-1}{4}} \ であり, \\\\ \angle \mathrm{BAC} \ は \ &\color{#0004fc}{鈍角} \ である. \end{align}$$

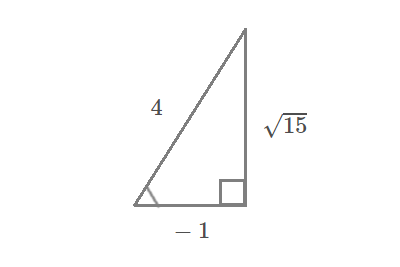
$$\sin \angle \mathrm{BAC}=\color{#0004fc}{\frac{\sqrt{15}}{4}}$$

問題

線分$ \ \mathrm{AC} \ $の垂直二等分線と直線$ \ \mathrm{AB} \ $の交点を$ \ \mathrm{D} \ $とする。
$ \ \cos \angle \mathrm{CAD}=\color{#0004fc}{\frac{ク}{ケ}} \ $であるから,$ \ \mathrm{AD}=\color{#0004fc}{コ} \ $　であり,
$ \ \triangle \mathrm{DBC} \ $の面積は$ \ \color{#0004fc}{\frac{サ\sqrt{シス}}{セ}} \ $である。

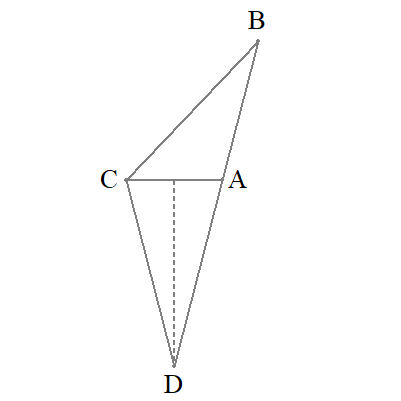
$$\begin{align} \cos \angle \mathrm{CAD}=&-\cos \angle \mathrm{CAB}=\color{#0004fc}{\frac{1}{4}} \end{align}$$

$$\begin{align}\cos \angle \mathrm{CAD}=&\frac{\mathrm{AH}}{\mathrm{DA}} \ より \\\\ \mathrm{AD}=&\color{#0004fc}{4} \end{align}$$
$$\begin{align}\triangle \mathrm{DBC} \ の面積を \ &\mathrm{S} \ とおく. \\\\ \mathrm{S}=&\frac{1}{2}\mathrm{AC}\sin \angle \mathrm{CAB}\left( \mathrm{AB}+\mathrm{AD}\right) \\\\ =&\frac{1}{2}\cdot 2\cdot \frac{\sqrt{15}}{4}\left( 3+4\right)\\\\ =&\color{#0004fc}{\frac{7\sqrt{15}}{4}} \end{align}$$

Lukia

問題自体は計算が主なので、公式を正確に覚えていれば、さほど問題はないと思います。
しかし、この問題をいかにスピーディに解けるかどうかの決め手は、ズバリ「図形$ \ \triangle \mathrm{ABC} \ $の正確さ」にかかっていると思います。
$ \ \angle \mathrm{BAD} \ $が鈍角とわかった時点で、図を描き改めておかないと、点$ \ \mathrm{D} \ $の位置を定められなくなります。

Lukia

第5問も幾何の問題ですが、コンパスや定規が持ち込み不可の大学入試センター試験において、なんとかいい方法はないもんか。と考えました。
もしかしたら、すでにやっている人がいるかもしれませんが、マークしたり、書いたりするための鉛筆（シャープペンシル）とは別に、使わない鉛筆を一本もっておいて、それを定規やコンパス代わりに使ってみるといいのではないかと思いました。

Lukia

「でも、目盛りがついてないよ！」という方があるかもしれませんね。
そこは、普段からの練習です。
1センチ、または0.5センチをフリーハンドで刻めるように、目（脳）を訓練しておくのです。
人間は、障害物があっても避けて通れますし、離れた人にボールを投げるとき、瞬時に距離や投げる力の強さなどを計算しています。
つまり、目測もくそくの能力を普段から使っているのです。
ということは、脳が学習するまでの一定期間をもうければ、定規なみの目盛りを打つことだって、不可能ではありません。
（実際、私は、0.5センチきざみで目盛りを刻んで、定規をあてたらピッタリだったことがあります）

Lukia

たとえば、今回の$ \ \triangle \mathrm{ABC} \ $も次のようにすれば、図を描くことは可能です。
まず、線分$ \ \mathrm{BC} \ $を目盛り4で線を引いておきます。
その線分で目盛り3をはかり、（鉛筆の先端がコンパスの鉛筆部分,先端から目盛り3にあたる鉛筆の軸をコンパスの針部分とみなします。）
針を指で固定して、半円を描き、
目盛り2も同様にすれば、その半円の交点が頂点$ \ \mathrm{A} \ $ということになりますね。

Lukia

また、お箸をクロスさせて持つのはお行儀が悪いことですが、鉛筆二本をお箸のように持ち、クロスさせて、同様に目盛りをはかれば、まさにコンパスのように円が描けます。
だいたいの交点（頂点）がほしいだけですから、これで十分ですよね。

Lukia

これを思いついたのが、またまた布団の中。（寝ているとよくいろんなことを思いつきます。）
初めは「指」をコンパス代わりにする。というアイディアだったのですが、もっとまっすぐで線が引きやすいもの。といえば、
鉛筆があるじゃん！と思いました。なるほど、これは合法的に正確な図形が描けるなぁ。と思ったものの、もう私は、「元・再受験生」の身。
自身のテストで活かせることはないでしょうね。
このセンター試験を解いてみるシリーズが完了したら、このアイディアの実践方法などを記事にしてみたいと思います。

2019年大学入試センター試験の数学の問題の一覧です。