高校数学の「絶対値と三角関数」に関する問題を解いてみる。(Yahoo!知恵袋より)

読了時間: 約10分22秒
[mathjax]
問題
\( \ \sin \theta=\vert \cos 3\theta \vert \ \)を満たすような\( \ \theta \ \)の\( \ 0 \leq \theta \leq \pi \ \)の解の個数を求めよ。
トリック・オア・トリート!
仕事帰りの電車で、暇つぶしのためYahoo!知恵袋アプリを開いたところ、おもしろそうな問題を見つけました。
おお、これはいい。記事にしよう。と思ったところ、
右辺にあの記号が・・・

Lukia
絶対値があるな。ってことは・・・

ディノ
トリック・オア・トリート!!

Lukia
にゃぁ〜〜〜、やっぱりぃ。。。

ディノ
おい、もう一回言うぜ?
トリック・オア・トリート!!
菓子くれよぉ〜。
トリック・オア・トリート!!
菓子くれよぉ〜。

Lukia
高校生にもなって、な〜にが、菓子くれよぉ。ですかッ!
今日という今日は、なんにもあげませんッ!
今日という今日は、なんにもあげませんッ!

ディノ
ふん。たまには、こっちから菓子やろうかと思ってたのに、残念だな。

Lukia
えっ、お菓子くれるんですか?ディノさんが?

ディノ
そうだよ。一緒に問題解かせてくれたら、礼しようかと思ってたけど、
そっか〜、いらないんなら、しょうがないか。
そっか〜、いらないんなら、しょうがないか。

Lukia
今日は、お菓子はあげない。とは言いましたが、
私がお菓子はいらない。とは言ってませんよ。(汗)
で、何?
何くれるんですか?
私がお菓子はいらない。とは言ってませんよ。(汗)
で、何?
何くれるんですか?

ディノ
それはあとのお楽しみだな。

Lukia
よ、よし。
じゃぁ、解いてみますか。
じゃぁ、解いてみますか。
まずは三角関数のおさらい。

Lukia
まずは、三角関数自体のおさらいをしてみましょう。
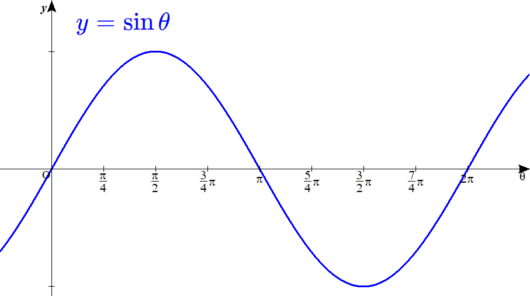
\( \ y=\sin \theta \ \)のグラフが以下の図のようになるのはよろしいでしょうか?
\( \ y=\sin \theta \ \)のグラフが以下の図のようになるのはよろしいでしょうか?

ディノ
おう、いいぞ!
習ったから、描けるぞ!
習ったから、描けるぞ!

Lukia
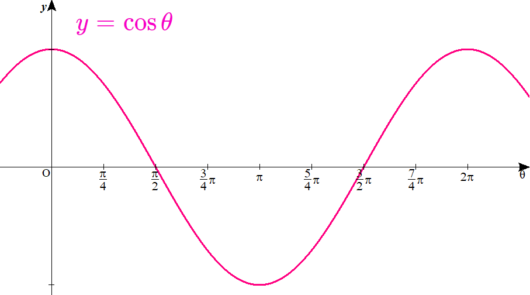
じゃ、\( \ y=\cos \theta \ \)のグラフをお願いしますね。

ディノ
おう。こうだな。

Lukia
いいですねぇ。
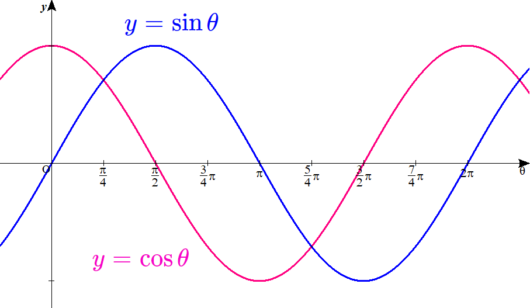
では、この\( \ y=\sin \theta \ \)と\( \ y=\cos \theta \ \)のグラフを重ねてみます。
では、この\( \ y=\sin \theta \ \)と\( \ y=\cos \theta \ \)のグラフを重ねてみます。

Lukia
重ねてみると、違いがわかりますね。

ディノ
そうだな。\( \ \theta=0 \ \)のとき、\( \ y=\sin \theta \ \)のグラフ\( \ y \ \)の値は\( \ 0 \ \)だけど、
\( \ y=\cos \theta \ \)のグラフの\( \ y \ \)の値は\( \ 1 \ \)になるよな。
\( \ y=\cos \theta \ \)のグラフの\( \ y \ \)の値は\( \ 1 \ \)になるよな。
山と谷の数を考える。

Lukia
まぁ、\( \ \theta=o \ \)を出発点とすると、値に差がありますよね。
逆にここはいっしょだな〜。と思うところはありますか?
逆にここはいっしょだな〜。と思うところはありますか?

ディノ
ずれてるけど、グラフの曲線の形が同じだ。

Lukia
そうですね。
次に\( \ y=\cos 3 \theta \ \)を考えるための導入となるんですが、グラフの横軸\( \ \theta \ \)軸を水平線とすると、
\( \ 0 \leq \theta \leq 2\pi \ \)の周期において、
\( \ y=\sin \theta \ \)または\( \ y=\cos \theta \ \)のグラフは、山と谷がそれぞれいくつありますか?
ただし、山については、ふもと(水平線)とふもと(水平線)に山頂が挟まれるようにして考えてくださいね。
次に\( \ y=\cos 3 \theta \ \)を考えるための導入となるんですが、グラフの横軸\( \ \theta \ \)軸を水平線とすると、
\( \ 0 \leq \theta \leq 2\pi \ \)の周期において、
\( \ y=\sin \theta \ \)または\( \ y=\cos \theta \ \)のグラフは、山と谷がそれぞれいくつありますか?
ただし、山については、ふもと(水平線)とふもと(水平線)に山頂が挟まれるようにして考えてくださいね。


ディノ
\( \ y=\sin \theta \ \)の場合は、水平線やふもとにあたる\( \ y=0 \ \)から始まって、山頂にいたり、その後下って再び水平線(またはふもと)にぶちあたるな。
んで、その後グラフは下り、谷底を経て、再び水平線に戻ってくる。
ということで、山も谷もひとつずつあるな。
んで、その後グラフは下り、谷底を経て、再び水平線に戻ってくる。
ということで、山も谷もひとつずつあるな。

ディノ
一方、\( \ y=\cos \theta \ \)のほうは・・・
谷は1つで間違いないけど、山は2つあるんじゃないのか?
谷は1つで間違いないけど、山は2つあるんじゃないのか?

Lukia
山についてはただし!って言ったことを思い出してください。ふもとから山頂、また再びふもとへ戻って、山1とカウントします。
考えにくかったら、頭の中でこのグラフを\( \ \theta=0 \ \)と\( \ \theta=2\pi \ \)で重ねて筒になるようにしてみてください。
すると、はたして山は2つですか?
考えにくかったら、頭の中でこのグラフを\( \ \theta=0 \ \)と\( \ \theta=2\pi \ \)で重ねて筒になるようにしてみてください。
すると、はたして山は2つですか?

ディノ
なるほど、重ねて筒状で考えれば、山はやっぱり1つしかないな。
3θは3倍速と考えればいい。

Lukia
\( \ 0 \leq \theta \leq 2\pi \ \)において、
\( \ y=\sin \theta \ \)も\( \ y=\cos \theta \ \)も、山と谷をそれぞれひとつずつ持つことがわかりました。
ちなみに、この山ひとつ、谷ひとつを「周期」と考えます。
\( \ y=\sin \theta \ \)も\( \ y=\cos \theta \ \)も、山と谷をそれぞれひとつずつ持つことがわかりました。
ちなみに、この山ひとつ、谷ひとつを「周期」と考えます。

Lukia
逆の言い方をすると、
\( \ 0 \leq \theta \leq 2\pi \ \)における、\( \ y=\sin \theta \ \)または\( \ y=\cos \theta \ \)の周期数は\( \ 1 \ \)ということができます。
\( \ 0 \leq \theta \leq 2\pi \ \)における、\( \ y=\sin \theta \ \)または\( \ y=\cos \theta \ \)の周期数は\( \ 1 \ \)ということができます。
![]()

Lukia
では、次に\( \ y=\cos 3\theta \ \)の周期数について考えてみましょう。

Lukia
さて、ディノさん、
「倍速」ってわかりますか?
なにか身近な「倍速」ってありませんか?
「倍速」ってわかりますか?
なにか身近な「倍速」ってありませんか?

ディノ
あ〜、動画サイトに「倍速」機能があるよな。
あれ、結構便利なんだ。
あれ、結構便利なんだ。

Lukia
なぜですか?どんなときに便利ですか?

ディノ
そうだなぁ。たとえば、ある動画を見たいんだけど、収録時間が10分あったとする。
でも、急いでるから、じっくり10分見られない。とか、
動画でしゃべってる人の口調がゆっくりだったり、ゆったりした動きのときは、倍速を上げて見たほうがストレスが少ないこともあるよな。
動画サイトには、最高で2倍速までの設定があるから、10分の動画も5分で見られることになる。
でも、急いでるから、じっくり10分見られない。とか、
動画でしゃべってる人の口調がゆっくりだったり、ゆったりした動きのときは、倍速を上げて見たほうがストレスが少ないこともあるよな。
動画サイトには、最高で2倍速までの設定があるから、10分の動画も5分で見られることになる。

Lukia
ということは、もしもう一本見たい動画があって、
その収録時間も10分だったとしたら?
その収録時間も10分だったとしたら?

ディノ
2倍速で連続してみれば、およそ10分で2本動画を見ることができるな。

Lukia
今の動画のたとえのディノさんの持ち時間「10分」を\( \ 0 \leq \theta \leq 2\pi \ \)と考え、
「倍速」を\( \ 3\theta \ \)の\( \ 3 \ \)と考えます。
「倍速」を\( \ 3\theta \ \)の\( \ 3 \ \)と考えます。

Lukia
\( \ 0 \leq \theta \leq 2\pi \ \)において、
\( \ y=\cos \theta \ \)は、山1、谷1で周期数は1でした。1「倍速」としておきましょうか。
では、\( \ 0 \leq \theta \leq 2\pi \ \)において、\( \ y=\cos 3\theta \ \)の周期数はいくつでしょうか。
\( \ y=\cos \theta \ \)は、山1、谷1で周期数は1でした。1「倍速」としておきましょうか。
では、\( \ 0 \leq \theta \leq 2\pi \ \)において、\( \ y=\cos 3\theta \ \)の周期数はいくつでしょうか。

ディノ
\( \ 3\theta \ \)ってことは、「3倍速」ってことだよな。
さっきの動画のたとえだと、もし、3倍速にする機能があれば、10分で収録時間10分の動画が3本見られることになる。
ということは、山と谷もそれぞれ3つ存在することになるな。
つまり、周期数は\( \ 3 \ \)だ!
さっきの動画のたとえだと、もし、3倍速にする機能があれば、10分で収録時間10分の動画が3本見られることになる。
ということは、山と谷もそれぞれ3つ存在することになるな。
つまり、周期数は\( \ 3 \ \)だ!
「周期」を意識してグラフを描こう。

Lukia
じゃ、\( \ y=\cos 3\theta \ \)のグラフ、描けますか?

ディノ
フリーハンドでそれぞれ3つの山と谷を描くのはしんどいな。

Lukia
たしかに。
じゃ、\( \ y=\cos 3\theta \ \)の「周期」を考えてみましょう。
\( \ y=\cos \theta \ \)の場合、\( \ \frac{ \pi }{ 2 } \leq \theta \leq {\frac{ 3 }{ 2 }}\pi \ \)で谷をつくり、
\( \ 0 \leq \theta \leq \frac{ \pi }{ 2 } \ \)と\( \ {\frac{ 3 }{ 2 }}\pi \leq \theta \leq 2\pi \ \)を合わせて山をつくっていました。
表現の仕方が難しいので、伝わりづらいかもしれませんが、ふもと(水平線)から\( \ \pi \ \)進む間に山をつくり、同様に水平線(ふもと)から\( \ \pi \ \)進む間に谷をつくります。
ということは、ふもとまたは水平線から\( \ \frac{ \pi }{ 2 } \ \)進んだところで山頂または谷底に到達しなければならないことになりますね。
じゃ、\( \ y=\cos 3\theta \ \)の「周期」を考えてみましょう。
\( \ y=\cos \theta \ \)の場合、\( \ \frac{ \pi }{ 2 } \leq \theta \leq {\frac{ 3 }{ 2 }}\pi \ \)で谷をつくり、
\( \ 0 \leq \theta \leq \frac{ \pi }{ 2 } \ \)と\( \ {\frac{ 3 }{ 2 }}\pi \leq \theta \leq 2\pi \ \)を合わせて山をつくっていました。
表現の仕方が難しいので、伝わりづらいかもしれませんが、ふもと(水平線)から\( \ \pi \ \)進む間に山をつくり、同様に水平線(ふもと)から\( \ \pi \ \)進む間に谷をつくります。
ということは、ふもとまたは水平線から\( \ \frac{ \pi }{ 2 } \ \)進んだところで山頂または谷底に到達しなければならないことになりますね。

ディノ
ということは、\( \ y=\cos 3\theta \ \)は、\( \ 0 \ \)から\( \ 2\pi \ \)の間を\( \ 3 \ \)つに区切って、
さらに\( \ 0 \ \)から\( \ 2\pi \ \)の間を\( \ 6 \ \)つに区切れば、山と谷にはさまれたふもと(水平線)の位置が決定できるな。
あ、でも、コサインの場合は、いきなり山頂から始まるから、6つじゃ、ふもと(水平線)の位置は決定できない。
\( \ 0 \ \)から\( \ 2\pi \ \)の間を\( \ 12 \ \)に区切る。
そうすると、
山頂→ふもと(水平線)→谷底→水平線(ふもと)→山頂・・・と目印が打てるから、
あとは曲線でつなげばいいわけだな。
さらに\( \ 0 \ \)から\( \ 2\pi \ \)の間を\( \ 6 \ \)つに区切れば、山と谷にはさまれたふもと(水平線)の位置が決定できるな。
あ、でも、コサインの場合は、いきなり山頂から始まるから、6つじゃ、ふもと(水平線)の位置は決定できない。
\( \ 0 \ \)から\( \ 2\pi \ \)の間を\( \ 12 \ \)に区切る。
そうすると、
山頂→ふもと(水平線)→谷底→水平線(ふもと)→山頂・・・と目印が打てるから、
あとは曲線でつなげばいいわけだな。

Lukia
すごい♪冴えてる〜♪
ということは、\( \ y=\cos 3\theta \ \)の「周期」は?
ということは、\( \ y=\cos 3\theta \ \)の「周期」は?

ディノ
\( \ 0 \ \)から\( \ 2\pi \ \)の間を\( \ 3 \ \)等分するんだから、
「周期」は\( \ {\frac{ 2 }{ 3 }}\pi \ \)だ。
「周期」は\( \ {\frac{ 2 }{ 3 }}\pi \ \)だ。
「周期」の感覚を叩き込む。

Lukia
ディノさん、すご〜い!
えっ、じゃぁ、じゃぁ、\( \ \sin 3\theta \ \)の周期は?
えっ、じゃぁ、じゃぁ、\( \ \sin 3\theta \ \)の周期は?

ディノ
そりゃ〜、\( \ {\frac{ 2 }{ 3 }}\pi \ \)だろ。

Lukia
正解ッ!
じゃぁ、じゃぁ、\( \ cos5\theta \ \)の周期は?
じゃぁ、じゃぁ、\( \ cos5\theta \ \)の周期は?

ディノ
\( \ {\frac{ 2 }{ 5 }}\pi \ \)。

Lukia
正解ッ!
じゃ、\( \ \sin 6\theta \ \)だったら?
じゃ、\( \ \sin 6\theta \ \)だったら?

ディノ
\( \ {\frac{ 2 }{ 6 }}\pi \ \)・・・
おっと、ひっかけやがったな。
\( \ \frac{ \pi }{ 3 } \ \)だ。
おっと、ひっかけやがったな。
\( \ \frac{ \pi }{ 3 } \ \)だ。

Lukia
うわ〜、ひっかからなかったか。(笑)
じゃぁ、じゃぁ〜。
\( \ 2\cos 3\theta \ \)!
じゃぁ、じゃぁ〜。
\( \ 2\cos 3\theta \ \)!

ディノ
へっ、\( \ 2\cos 3\theta \ \)?
(見る場所は、\( \ \theta \ \)のあるところだけだから・・・)
くっ・・・、さ、\( \ {\frac{ 2 }{ 3 }}\pi \ \)!
(見る場所は、\( \ \theta \ \)のあるところだけだから・・・)
くっ・・・、さ、\( \ {\frac{ 2 }{ 3 }}\pi \ \)!

Lukia
にゃ〜ッ、しびれちゃうぅ〜♪
はっ、失礼しました。(笑)
じゃ、これが最後の質問です。
\( \ \sin \frac{1}{2}\theta \ \)の周期は?

ディノ
ええ?にぶんのいち???
\( \ \frac{2\pi}{\frac{1}{2}} \ \)ってことは、にぃぱい わる にぶんのいち・・・
わ〜 にぃぱい かけ に ってことだから・・・
\( \ 4\pi \ \)!!
\( \ \frac{2\pi}{\frac{1}{2}} \ \)ってことは、にぃぱい わる にぶんのいち・・・
わ〜 にぃぱい かけ に ってことだから・・・
\( \ 4\pi \ \)!!

Lukia
完璧ですっ!
珍しくディノさんが翻弄されてましたね。たまにはこういうのもいいかな。
グラフ上の絶対値表記を考える。

Lukia
「周期」や「周期数」の感覚がそなわり、グラフが楽に描けるようになったところで、いよいよ絶対値の意味を考えていきたいと思います。

Lukia
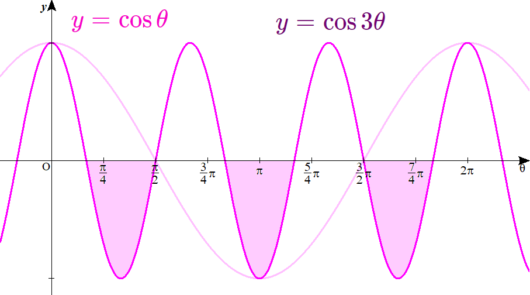
さきほど、ディノさんが描いてくれた\( \ y=\cos 3\theta \ \)のグラフを見てみましょう。


Lukia
横軸、今回は\( \ \theta \ \)軸となっていますが、ここが\( \ y=0 \ \)にあたりますよね。
曲線が\( \ \theta \ \)軸よりも下にある場合、\( \ y \ \)の値は・・・
曲線が\( \ \theta \ \)軸よりも下にある場合、\( \ y \ \)の値は・・・

ディノ
負になるな。

Lukia
そうですね。
グラフでは負になる部分をピンクで塗りつぶしています。
グラフでは負になる部分をピンクで塗りつぶしています。

Lukia
でも、今回考えるのは、
\( \ y=\vert \cos 3\theta \vert \ \)ですよね。
ということは、ピンクに塗りつぶした部分は・・・
\( \ y=\vert \cos 3\theta \vert \ \)ですよね。
ということは、ピンクに塗りつぶした部分は・・・

ディノ
このままじゃまずいな。絶対値は、0までの距離と考えると、距離に負はありえないもんな。

Lukia
では、どうすればいいですか?

ディノ
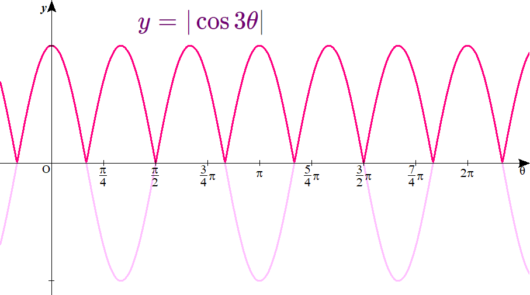
ピンクに塗りつぶした部分を\( \ \theta \ \)軸で折り返す!
つまりこうなる!
つまりこうなる!

Lukia
まぁ、なんて仕事の速い!
濃いピンクの曲線で、すべて山になっていますね。
絶対値山脈とでも名付けたくなるような。
濃いピンクの曲線で、すべて山になっていますね。
絶対値山脈とでも名付けたくなるような。

ディノ
折り返したものがわかりやすいよう、元・負の値だった曲線部分は、淡いピンクで残像のように描いておいたぞ。

Lukia
ナイスです。
解の個数を求める。

Lukia
それでは、いよいよ仕上げです。
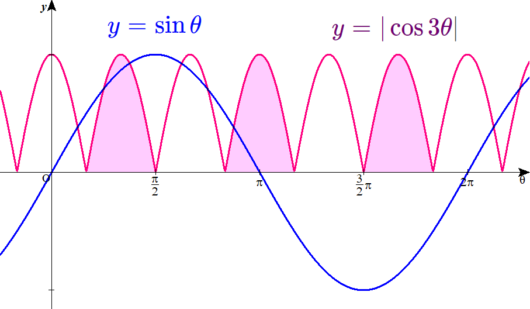
\( \ y=\sin \theta \ \)と\( \ y=\vert \cos 3\theta \vert \ \)のグラフを重ねて描いてみましょう。
\( \ y=\sin \theta \ \)と\( \ y=\vert \cos 3\theta \vert \ \)のグラフを重ねて描いてみましょう。

ディノ
\( \ \theta \ \)軸で折り返した部分は、またピンクで塗りつぶしたぞ。

Lukia
はい。
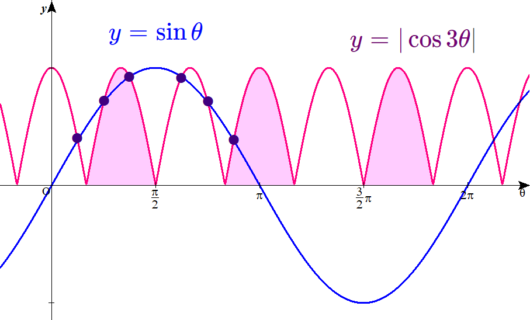
すなわち、\( \ 0 \ \)から\( \ \pi \ \)の範囲における青い曲線の\( \ \sin \theta \ \)とピンクの曲線の\( \ \vert \cos 3\theta \vert \ \)交点の個数が、
求める「解の個数」となりますね。
わかりやすいよう紫の点をつけてみます。
すなわち、\( \ 0 \ \)から\( \ \pi \ \)の範囲における青い曲線の\( \ \sin \theta \ \)とピンクの曲線の\( \ \vert \cos 3\theta \vert \ \)交点の個数が、
求める「解の個数」となりますね。
わかりやすいよう紫の点をつけてみます。

ディノ
6個あるな。

Lukia
そのとおり!

トリック・オア・トリート!再び。

Lukia
解けましたね。今回、5800字も書いてますから、
数学カテゴリにしては超大作ですよ。
数学カテゴリにしては超大作ですよ。

ディノ
そうだな。問題自体はシンプルなのに、中身は結構ハードだったよな。

Lukia
んで、何食べさせてくれるんですか?

ディノ
お、おう・・・。
これだ。
これだ。
ぶっきらぼうに渡された紙袋を開けてみると・・・


Lukia
うわ〜、プリンだぁ〜〜♪

ディノ
ほら、こないだ、プリン好きだって言ってたろ?

Lukia
優しいとこあるんですねっ♪

ディノ
ふんっ、さっさと食えっ!(汗)
照れるディノさんを眺めつつ、おいしくいただいたのでした。
こたえ
解:6つ
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません