高校数学の「空間ベクトルの内積（外積を利用）」に関する問題を解いてみる。（Yahoo!知恵袋より）

アを求める。

$$\begin{align}\vec{a}\cdot \vec{b}=&1\cdot t+\left( -t\right)\cdot \left( -1\right)+\left( -1\right) \cdot 1\\\\ =&t+t-1 \\\\ =&2t-1 \end{align}$$

イを求める。

$$\begin{align}\frac{\vec{a}\cdot \vec{b}}{\vert \vec{a} \vert\vert \vec{b} \vert}=&\cos {\frac{ 2 }{ 3 }}\pi \\\\ \\\\ \frac{2t-1}{\sqrt{t^2+2}\sqrt{t^2+2}}=&-\frac{1}{2} \\\\ \\\\ -2\left( 2t-1\right)=&t^2+2\\\\ t\left( t+4\right)=&0\\\\ t=&-4\quad \left( t \neq 0\quad より\right) \end{align}$$

ウを求める。

Lukia

現在は高校数学で、ベクトルの外積というのを教えなくなっているようなのですが、「ふたつのベクトルに垂直な」ベクトルを求めるときには、とても便利なので、覚えておくとよいかもしれません。

\( \ \vec{a}=\left( a \ , \ b \ , \ c\right) \ \) \( \ \vec{b}=\left( s \ , \ t \ , \ u\right) \ \)のとき

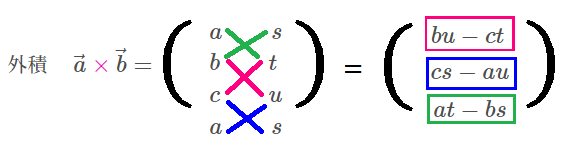
$$\begin{align}\vec{c}=&\vec{a}\times \vec{b}=\left( 3 \ , \ 3 \ , \ 15\right)=3k\left( 1 \ , \ 1 \ , \ 5\right)\quad \left( k \ は実数\right) \\\\ また \ \vert \vec{c} \vert=&1\quad より \\\\ \vert \vec{c} \vert=&3k\sqrt{1^2+1^2+5^2}=9\sqrt{3}k=1\\\\ \\\\ k=& \pm \frac{\sqrt{3}}{27}\\\\ \\\\ ゆえに, \ \vec{c}=& \pm \frac{\sqrt{3}}{9}\left( 1 \ , \ 1 \ , \ 5\right) \end{align}$$

$$\begin{align}\vert \vec{c}\cdot \vec{d} \vert=&\vert \pm \frac{\sqrt{3}}{9}\left( 1 \ , \ 1 \ , \ 5\right)\cdot \left( 0 \ , \ 0 \ , \ 1\right) \vert \\\\ \\\\ =&\frac{5\sqrt{3}}{9}\end{align}$$

ウの解法（本当はこっち）

$$\begin{align}\vec{c}=&\left( x \ , \ y \ , \ z\right)\quad とし \\\\ &\sqrt{x^2+y^2+z^2}=1\quad とする。\\\\ \vec{a}\cdot \vec{c}=&0\quad より\\\\ &x+4y-z=0\quad \cdots\cdots \ ① \\\\ \vec{b}\cdot \vec{c}=&0\quad より\\\\ &-4x-y+z=0\quad \cdots\cdots \ ②\\\\ ①と②より&x=y\quad ,\quad z=5y\quad である。\\\\ x^2+y^2+z^2=&y^2+y^2+25y^2=1\quad より\\\\ y=& \pm \frac{\sqrt{3}}{9}\\\\ \\\\ ゆえに,\quad &\vec{c}= \pm \frac{\sqrt{3}}{9}\left( 1 \ , \ 1 \ , \ 5\right) \end{align}$$
(以下略）

こたえ

$$\begin{align}\color{#0004fc}{ア}\quad &2t-1 \\\\ \color{#0004fc}{イ}\quad &-4 \\\\ \color{#0004fc}{ウ}\quad &\frac{5\sqrt{3}}{9} \end{align}$$