高校数学の「円の方程式」に関する問題を解いてみる。(Yahoo!知恵袋より)

私の解き方

Lukia
すっごい時間もかかるし、紙も要します。
解き終わったらヘトヘト・・・。

Lukia

Lukia
$$\begin{align}\left( x+1\right)^2+\left( y+2\right)^2-1-4-4=&0 \\\\ \left( x+1\right)^2+\left( y+2\right)^2=&3^2\quad \cdots\quad ☆ \\\\ ☆は中心\left( -1 \ , \ -2\right) \quad &\quad 半径 \ 3 \ の円\end{align}$$
$$\begin{align}7x-y+2=&0\quad より \\\\ y=&7x+2\quad を☆に代入. \\\\ \left( x+1\right)^2+\left( 7x+4\right)^2=&9 \\\\ 50x^2+58x+8=&0\\\\ x=-1\quad ,&\quad x=-\frac{4}{25} \end{align}$$
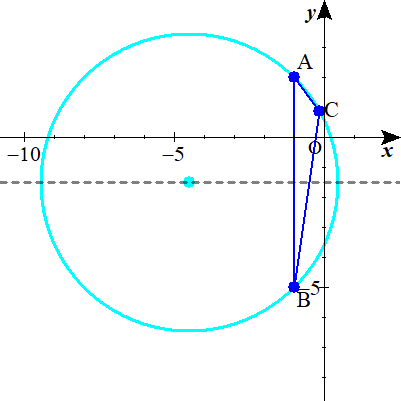
円と直線の交点を B , C とすると,
$$\begin{align}\mathrm{B}& \ \left( -1 \ , \ -5\right)\\\\ \mathrm{C}& \ \left( -\frac{4}{25} \ , \ \frac{22}{25}\right) \quad である.\\\\ 点\mathrm{A}を& \ \left( -1 \ , \ 2\right) \quad とする.\end{align}$$

三角形ABCの外心は各辺の垂直二等分線の交点である.
$$\begin{align}辺\mathrm{AB}&は直線\quad x=-1\quad 上にあり, \\\\ 中点は& \ \left( -1 \ ,-\frac{3}{2}\right)\quad であるから, \\\\ 求める円を&\quad \left( x-\alpha\right)^2+\left( y-\beta\right)^2=r^2\quad \left( \alpha \ , \ \beta \ , \ rは実数.特にr \gt 0\right)\quad とすると,\\\\ \beta=&-\frac{3}{2}\quad である.\\\\ &\left( x-\alpha\right)^2+\left( y+\frac{3}{2}\right)^2=r^2\quad である. \end{align}$$
$$\begin{align}辺\mathrm{BC}は&傾き7の直線上にあるので,\\\\ 円の中心と&辺\mathrm{BC}の中点を結ぶ直線の傾きは\quad -\frac{1}{7}\quad である. \end{align}$$
$$\begin{align}\frac{-\frac{3}{2}-\frac{\mathrm{B}_y+\mathrm{C}_y}{2}}{\alpha-\frac{\mathrm{B}_x+\mathrm{C}_x}{2}}=&-\frac{1}{7} \\\\ \ \frac{3+\mathrm{B}_y+\mathrm{C}_y}{2\alpha-\mathrm{B}_x-\mathrm{C}_x}=&\frac{1}{7} \\\\ \ 21+7\mathrm{B}_y+7\mathrm{C}_y+\mathrm{B}_x+\mathrm{C}_x=&2\alpha\\\\ \ 21-1-35-\frac{4}{25}+\frac{7\times 22}{25}=&2\alpha\\\\ \alpha=&-\frac{9}{2} \end{align}$$

ゆえに,
$$\begin{align}\left( x+\frac{9}{2}\right)^2+\left( y+\frac{3}{2}\right)^2=&r^2 \\\\ これに \ &\mathrm{A}\left( -1 \ , \ 2\right) \ を代入して, \\\\ \left( \frac{7}{2}\right)^2+\left( \frac{7}{2}\right)^2=&r^2\\\\ r^2=&\frac{49}{2}\ \\\\ 求める円は,&\quad \left( x+\frac{9}{2}\right)^2+\left( y+\frac{3}{2}\right)^2=\frac{49}{2} \end{align}$$

Lukia
まず、直線と円との交点を求め、
外接円の中心(外心)の特性から円の中心を求め、
円周上の一点を代入して半径を求める。
チョ~めんどくさいでしょ?(笑)

Lukia
しかし、こういう2行ほどで終わってしまうような問題は、大問のかなり序盤の小問であることが多いです。
序盤の小問にこんなにも時間も紙も労力も使っていたら、先が思いやられますね。というわけで、以下のやり方も知っておきましょう。
曲線束の応用を用いて楽に解く。
求める円の方程式を,
$$\begin{align}x^2+y^2+2x+4y-4+\color{#0004fc}{k}\left( 7x-y+2\right)=&0\quad \left( kは実数\right) \quad とおく.\\\\ この円は\quad \left( -1 \ , \ 2\right) \quad を通るから,&\\\\ 1+4-2+8-4+\color{#0004fc}{k}\left( -7-2+2\right)=&0\\\\ これを解いて,\\\\ \quad k=1&\\\\ \ x^2+y^2+2x+4y-4+7x-y+2=&0\\\\ これを整理して,&\quad\\\\ \left( x+\frac{9}{2}\right)^2+\left( y+\frac{3}{2}\right)^2=&\frac{49}{2} \end{align}$$

Lukia
あっという間に終わってしまったような気がします。
しかし、実際この問題、曲線束を用いるということはわかっていても、計算間違いをしてしまい、
「問題の数値、あってますか?」と逆に質問者に質問する回答者さんが続出しました。
求める円の中心の座標が分数(しかもマイナスつき)だったので、計算間違いが出やすかったんだと思います。

Lukia
基本をおさえることを忘れないようにしたいものですね。
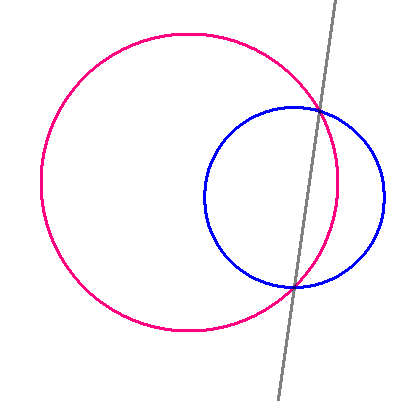
今後の役に立ちそうなこと。
$$\begin{align}2つの円\quad \mathrm{C1}と\mathrm{C2}が&\\\\ \color{#f700ca}{\mathrm{C}1} \ :\quad &\color{#f700ca}{x^2+y^2+ax+by+c=0} \\\\ \color{#0004fc}{\mathrm{C}2} \ :\quad &\color{#0004fc}{x^2+y^2+sx+ty+u=0}\quad で示されるとき, \\\\ &\color{#f700ca}{x^2+y^2+ax+by+c}+k\left( \color{#0004fc}{x^2+y^2+sx+ty+u}\right)=0\quad \left( kは実数\right)\quad は\\\\ &k \ の値にかかわらず,2交点を通る円を表す.\\\\ \ 特に,\quad k=-1& \ のとき,2交点を通る直線を表す.\\\\ k=0& \ のとき,円\color{#f700ca}{C1} \quad を表す.\\\\ &\quad \left( 円\mathrm{\color{#0004fc}{C2}}\quad は\color{#0004fc}{表せない}.\right) \end{align}$$
こたえ
$$\left( x+\frac{9}{2}\right)^2+\left( y+\frac{3}{2}\right)^2=\frac{49}{2}$$
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません