高校数学の「線形計画法」に関する問題を解いてみる。(Yahoo!知恵袋より)

製品AとBは、それぞれ1トン作るのに、以下の表のとおり材料P,Qを必要とする。
さらに、販売価格は製品A,Bの1トン当たりの金額である。
| 材料P | 材料Q | 販売価格 | |
| 製品A | 3トン | 1トン | 2万円 |
| 製品B | 1トン | 2トン | 1万円 |
材料Pが一日当たり最大9トンまで、また、材料Qが一日当たり最大8トンまで仕入れることができるとき、
一日当たりの販売価格を最大にするには、製品Aと製品Bをそれぞれ何トン作ればよいか。

Lukia
うれしげにもう一問解いてみようと思います。(笑)
製品Aは、Aトン/日 製造され、
製品Bは、Bトン/日 製造されるものとする。
この工場の一日の売り上げ価格は、2A+B (万円)と表される。
材料Pは、一日当たり 3A+B トン必要であり、
材料Qは、一日当たり A+2B トン必要である。
$$\begin{align}以上より、&\mathrm{A} \geq 0\quad \cdots\cdots\quad ① \\\\ &\mathrm{B} \geq 0\quad \cdots\cdots\quad ② \\\\ 0 \leq &\mathrm{P} \leq 9\quad \cdots\cdots\quad ③\\\\ 0 \leq &\mathrm{Q} \leq 8\quad \cdots\cdots\quad ④ \end{align}$$
③より
$$\begin{align}0 \leq &\mathrm{P} \leq 9 \\\\ 0 \leq &3\mathrm{A}+\mathrm{B} \leq 9\end{align}$$
④より
$$\begin{align}0 \leq &\mathrm{Q} \leq 8\\\\ 0 \leq &\mathrm{A}+2\mathrm{B} \leq 8\end{align}$$
$$ここで,\quad \mathrm{A}=x\quad ,\quad \mathrm{B}=y\quad とおく.$$
①~④は,
$$\begin{align}&x \geq 0\quad \cdots\cdots\quad ① \\\\ &y \geq 0\quad \cdots\cdots\quad ② \\\\ 0 \leq &3x+y \leq 9\quad \cdots\cdots\quad ③\\\\ 0 \leq &x+2y \leq 8\quad \cdots\cdots\quad ④ \end{align}$$
と表される.
また、この工場の一日当たりの売り上げ価格を
$$2x+y=k\quad \left( kは\quad k \gt 0 \ の実数\right)\quad \cdots\cdots\quad ⑤とおく.$$
①~④で示される領域は以下の図のピンク色で塗りつぶされた部分。(境界は含まれる)
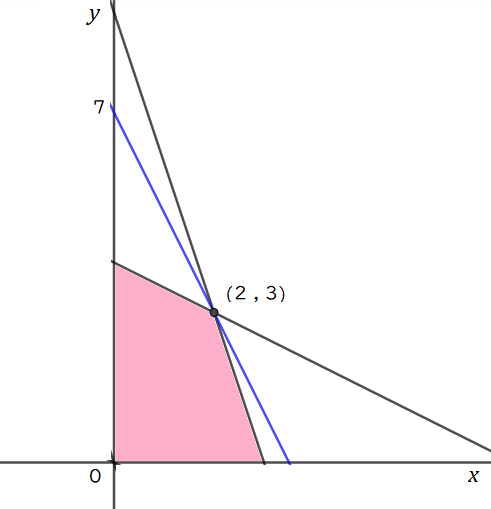
$$\begin{align}⑤を変形して,&\quad y=-2x+k\quad とすると \\\\ k& \ の最大値は,点\left( 2 \ , \ 3\right)\quad を通るときに得られる. \\\\ 3=&-2\times 2+k\\\\ すなわち,&\quad k=7 \end{align}$$
以上より, 一日当たり 製品Aを2トン, 製品Bを3トン 製造すればよい.
こたえ
| 製品A | 製品B |
| 2トン | 3トン |
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません