高校数学の「空間ベクトルとその内分比」に関する問題を解いてみる。（Yahoo!知恵袋より）
読了時間: 約2分5秒
[mathjax]
問題
1辺の長さが\(1\)の四面体\(\mathrm{OABC}\)において、
辺\(\mathrm{OA}\)を\(1:2\)に内分する点を\(\mathrm{P}\)とし、
辺\(\mathrm{BC}\)を\(1:3\)に内分する点を\(\mathrm{Q}\)とする。
また、線分\(\mathrm{PQ}\)の中点を\(\mathrm{M}\)とする。
\(\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{a}} \ , \ \overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{b}} \ , \ \overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{c}}\)とするとき、
\(\overrightarrow{\mathrm{OM}}\)を\(\overrightarrow{\mathrm{a}} \ , \ \overrightarrow{\mathrm{b}} \ , \ \overrightarrow{\mathrm{c}}\)を用いて表せ。
辺\(\mathrm{OA}\)を\(1:2\)に内分する点を\(\mathrm{P}\)とし、
辺\(\mathrm{BC}\)を\(1:3\)に内分する点を\(\mathrm{Q}\)とする。
また、線分\(\mathrm{PQ}\)の中点を\(\mathrm{M}\)とする。
\(\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{a}} \ , \ \overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{b}} \ , \ \overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{c}}\)とするとき、
\(\overrightarrow{\mathrm{OM}}\)を\(\overrightarrow{\mathrm{a}} \ , \ \overrightarrow{\mathrm{b}} \ , \ \overrightarrow{\mathrm{c}}\)を用いて表せ。
与えられた情報を図にまとめる。
Lukia
四面体\(\mathrm{OABC}\)と、内分比を図にしました。
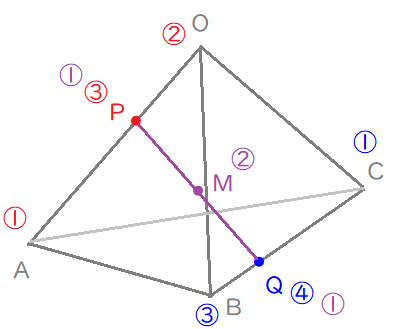
内分比を「統一」する。
Lukia
内分比を「統一」していきます。
赤は4倍、青は3倍、紫は12倍すればいいことになりますね。
赤は4倍、青は3倍、紫は12倍すればいいことになりますね。
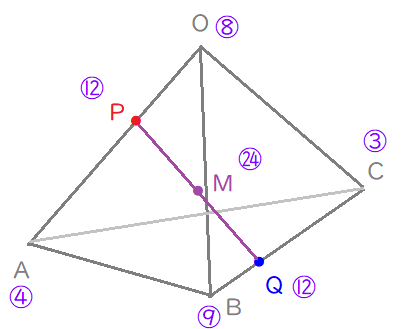
各点の「比」を書き出す。
Lukia
あとは、点\(\mathrm{M}\) , 点\(\mathrm{A}\) , 点\(\mathrm{B}\) , 点\(\mathrm{C}\) 上にある比を書き出していくだけです。
$$\begin{align}24\overrightarrow{\mathrm{OM}}=&4\overrightarrow{\mathrm{a}}+9\overrightarrow{\mathrm{b}}+3\overrightarrow{\mathrm{c}} \\\\ \\\\ \overrightarrow{\mathrm{OM}}=&\frac{1}{24}\left( 4\overrightarrow{\mathrm{a}}+9\overrightarrow{\mathrm{b}}+3\overrightarrow{\mathrm{c}}\right) \end{align}$$
Lukia
分母を統一したままにしておくため、ベクトルをカッコでくくっていますが、かっこを開いて、それぞれ分数とベクトルの形に直してもいいと思います。その際、約分のし忘れや、そもそも計算間違いなどをしないように注意してくださいね。
これらの危険性を回避するためにも、ここで留めおくほうが無難です。
これらの危険性を回避するためにも、ここで留めおくほうが無難です。
こたえ
$$\overrightarrow{\mathrm{OM}}=\frac{1}{24}\left( 4\overrightarrow{\mathrm{a}}+9\overrightarrow{\mathrm{b}}+3\overrightarrow{\mathrm{c}}\right)$$
共有:
プロフィール
Author Profile
