高校数学の「放物線と直線の共有点とその距離」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年2月24日2023年1月14日二次関数実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

4つの交点を明らかにする。

$$\begin{align}曲線\mathrm{C}_1 \ と\quad &y=k\quad の交点のx座標を求める. \\\\ \left( x-3\right)^2=&k\quad より, \\\\ x=&3 \pm \sqrt{k} \\\\ 曲線\mathrm{C}_2 \ と\quad &y=k\quad の交点のx座標を求める.\\\\ \left( x-1\right)^2=&k\quad より, \\\\ x=&1 \pm \sqrt{k}\end{align}$$

0＜k＜1 のとき

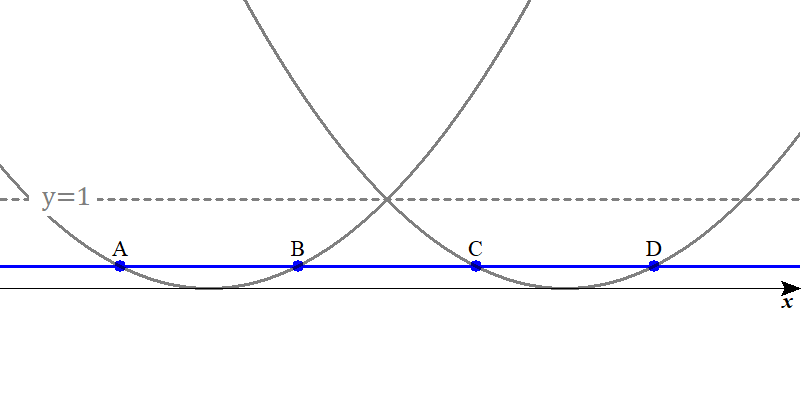
$$\begin{align}0 \lt k \lt 1\quad &のとき,4点\mathrm{A} \ , \ \mathrm{B} \ ,  \  \mathrm{C} \ , \ \mathrm{D} は,\\\\ 左から\quad &\mathrm{A}\left( 1-\sqrt{k} \ , \ k\right)\quad ,\quad \mathrm{B}\left( 1+\sqrt{k} \ , \ k\right)\\\\ & \mathrm{C}\left( 3-\sqrt{k} \ , \ k\right)\quad ,\quad \mathrm{D}\left( 3+\sqrt{k} \ , \ k\right)\quad と並んでいる. \end{align}$$
4点 A , B , C , D が等間隔に並んでいるということは、
AD間が点B, 点C によって3等分されているといえる。

$$\begin{align}\frac{\mathrm{AD}}{3}=&\mathrm{BC} \\\\ \mathrm{AD}=&3\mathrm{BC} \\\\ 3+\sqrt{k}-1+\sqrt{k}=&3-\sqrt{k}-1-\sqrt{k} \\\\ 2+2\sqrt{k}=&6-6\sqrt{k}\\\\ \sqrt{k}=&\frac{1}{2}\\\\ k=&\frac{\color{#0004fc}{1}}{\color{#0004fc}{4}} \end{align}$$

1＜k のとき

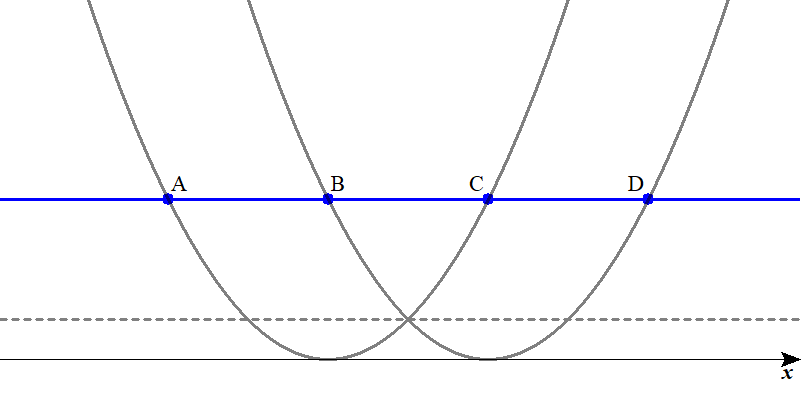
$$\begin{align}1 \lt k \quad &のとき,4点\mathrm{A} \ , \ \mathrm{B} \ , \ \mathrm{C} \ , \ \mathrm{D} は,\\\\ 左から\quad &\mathrm{A}\left( 1-\sqrt{k} \ , \ k\right)\quad ,\quad \mathrm{B}\left( 3-\sqrt{k} \ , \ k\right)\\\\ & \mathrm{C}\left( 1+\sqrt{k} \ , \ k\right)\quad ,\quad \mathrm{D}\left( 3+\sqrt{k} \ , \ k\right)\quad と並んでいる. \end{align}$$
4点 A , B , C , D が等間隔に並んでいるということは、
AD間が点B, 点C によって3等分されているといえる。
$$\begin{align}\frac{\mathrm{AD}}{3}=&\mathrm{BC} \\\\ \mathrm{AD}=&3\mathrm{BC} \\\\ 3+\sqrt{k}-1+\sqrt{k}=&3\left( 1+\sqrt{k}-3+\sqrt{k}\right) \\\\ 2+2\sqrt{k}=&-6+6\sqrt{k} \\\\ \sqrt{k}=&2\\\\ k=&\color{#0004fc}{4} \end{align}$$

こたえ

$$\begin{align}0 \lt k \lt 1 \quad のとき\quad &k=\frac{\color{#0004fc}{1}}{\color{#0004fc}{4}}\\\\
k \gt 1\quad のとき\quad &k=\color{#0004fc}{4}\end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。