高校数学の「データの分析(値の推定）」に関する問題を解いてみる。（Yahoo!知恵袋より）
問題
ただし,\( \ a \leqq b \ \)とする。
\( \ 5 \ , \ 2 \ , \ 3 \ , \ 8 \ , \ 6 \ , \ 3 \ , \ 7 \ , \ 6 \ , \ a \ , \ b \ \)
わかっていることを書き出しておく。
$$\begin{align}個々のデータを\quad &x_i\quad \left( i=1 \ , \ 2 \ , \ \cdots \ , \ 10\right)\quad とする. \\\\ 平均を\quad &\overline{x}\quad とすると, \\\\ \overline{x}=&\frac{1}{10}\sum_{i=1}^{10}{x_i}=5\quad \cdots\cdots\quad ① \ と表せる.\\\\ また,偏差を\quad &x_i-\overline{x}\quad とする.\\\\ 特に\quad &a \ の偏差を\quad \alpha\quad \left( \alpha \geqq 0\right)\\\\ &b \ の偏差を\quad \beta\quad \left( \beta \geqq 0\right) \quad とする.\\\\ ここで,\quad &a \leqq b\\\\ &a-\overline{x} \leqq b-\overline{x}\\\\ &\alpha \leqq \beta\quad が成り立つとする. \\\\ さらに,分散を\quad &s^2\quad とする.\\\\ s^2=&\frac{1}{10}\sum_{i=1}^{10}{\left( x_i-\overline{x}\right)^2}=5\quad \cdots\cdots\quad ② \ と表せる。 \end{align}$$
仮のキャタピラー表をかいちゃおう。
Lukia
「キャタピラー表」と命名いたしました。
今回、すでに平均が\( \ 5 \ \)とわかっているので、数字によってあらわされているデータを上下に振り分けるのは簡単にできると思いますが、
問題は、\( \ a \ , \ b \ \)の偏差をどうすればいいか。ということですよね。
Lukia
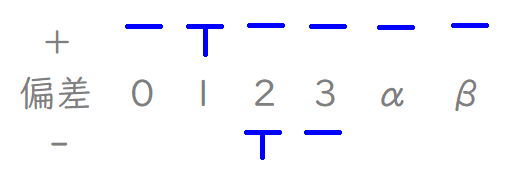
$$\begin{align}\frac{1}{10}\sum_{i=1}^{10}{\left( x_i-\overline{x}\right)}=&\frac{1}{10}\sum_{i=1}^{10}{x_i}-\frac{10\overline{x}}{10}\\\\ =&\overline{x}-\overline{x}=0\quad より\end{align}$$
$$\begin{align} 1\times 2+2\times 1+\left( -2\right)\times 2+3\times 1+\left( -3\right)\times 1+\alpha+\beta=&0 \\\\ \alpha+\beta=&0\\\\ ここで,\quad \alpha \leqq \beta \ の仮定より,\quad \alpha=-\beta&\quad とする.\end{align}$$
分散の式を立てて方程式を解く。
Lukia
すると、以下のとおりになりますね。
$$\begin{align} ②式\quad &より\\\\ s^2=&\frac{1}{10}\lbrace1^2\times 2+2^2\times 3+3^2\times 2+\left( -\beta\right)^2\times 1+\beta^2\times 1 \rbrace=5 \\\\ 両辺を10倍して,& \\\\ &32+2\beta^2=50\\\\ &\beta^2=9 \\\\ &\beta \geqq 0\quad より\\\\ &\beta=3\\\\ ゆえに,\quad &\alpha=-3\quad \left( \alpha \leqq \beta\quad の仮定も成り立つ.\right)\end{align}$$
以上より,
$$\begin{align}a=&\alpha+\overline{x}=-3+5=2 \\\\ b=&\beta+\overline{x}=3+5=8 \end{align}$$
こたえ
$$a=2\quad ,\quad b=8$$
